In the xy-plane, the length of the shortest path from (0,0) to (12,16) that does not go inside the circle ${(x - 6)}^{2} + {(y - 8)}^{2} = 25$ is
$10 \sqrt{3}$
$10 \sqrt{5}$
$10 \sqrt{3} + \frac{5 π}{3}$
$10 + 5 π$ Solution in Bengali

A

$10 \sqrt{3}$

B

$10 \sqrt{5}$

C

$10 \sqrt{3} + \frac{5 π}{3}$

D

$10 + 5 π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let $O \equiv (0, 0) P \equiv (6, 8)$ and $Q \equiv (12, 16)$ .
As shown in the figure, the shortest route consists of tangent OT, minor arc TR and tangent RQ.
Since $O P = 10, P T = 5$ , and $∠ O T P = 90^{\circ}$ , it follows that $∠ O P T = 60^{\circ}$ and $O T = 5 \sqrt{3}$ .

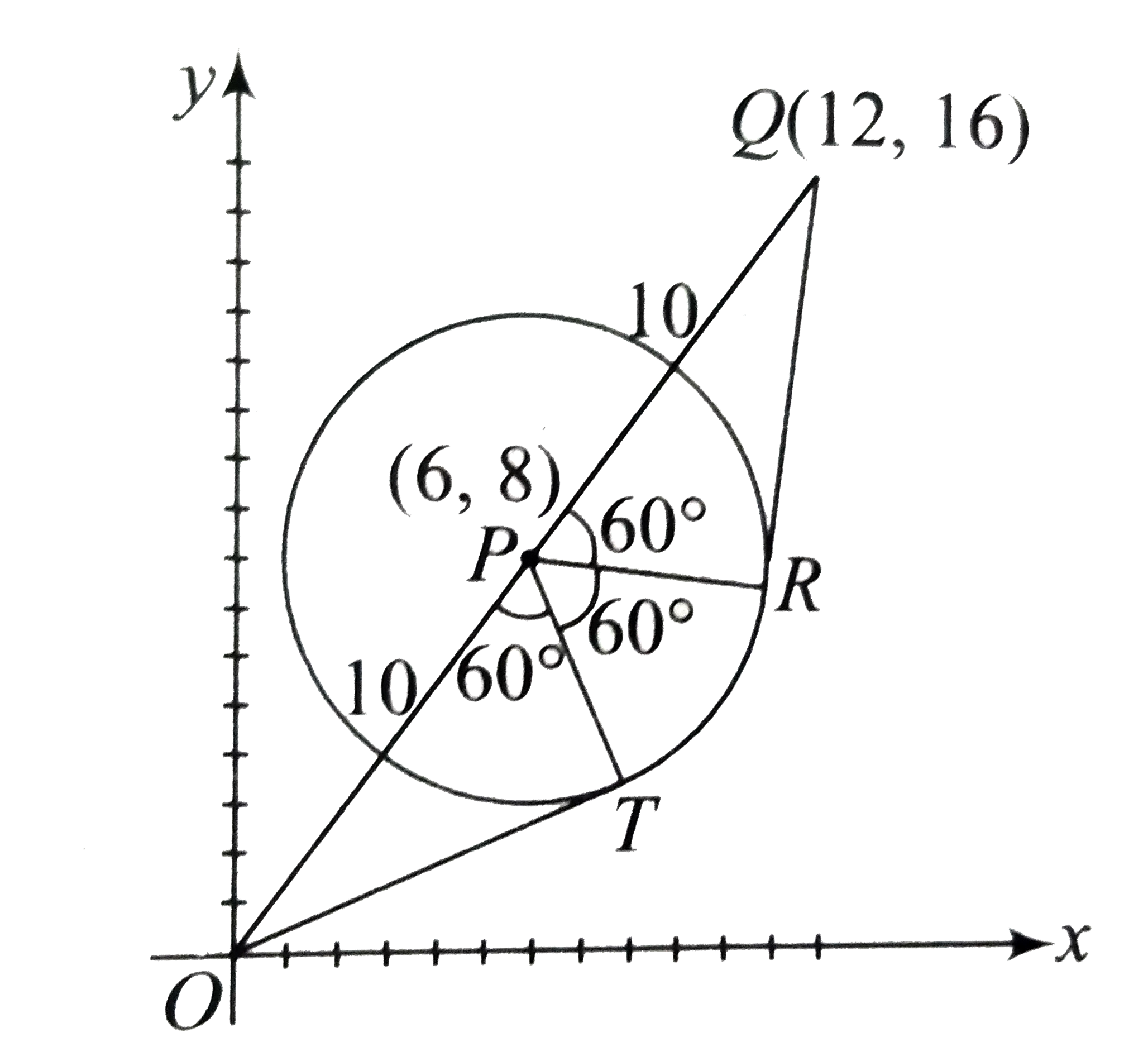
Similarly, $P Q = 10$ and $P R = 5$
$∴ ∠ Q P R = 60^{\circ}$ and $Q R = 5 \sqrt{3}$
Also points O,P and Q are collinear as $m_{O P} = m_{P Q}$
Thus, $∠ R P T = 60^{\circ}$ and arc TR is of length $\frac{5 π}{3}$ .
Hence, the length of the shortest route is $2 (5 \sqrt{3}) + \frac{5 π}{3}$ .

Updated on:21/07/2023

|

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-CIRCLES-Comprehension Type

Home
Ask Doubt
Profile