AB is a line segment of length 48 cm and C is its mid-point. If three semicircles are drawn at AB, AC and CB using as diameters, then radius of the circle inscribed in the space enclosed by three semicircles is Solution in Bengali
3√2
6
8
10
The correct Answer is:C
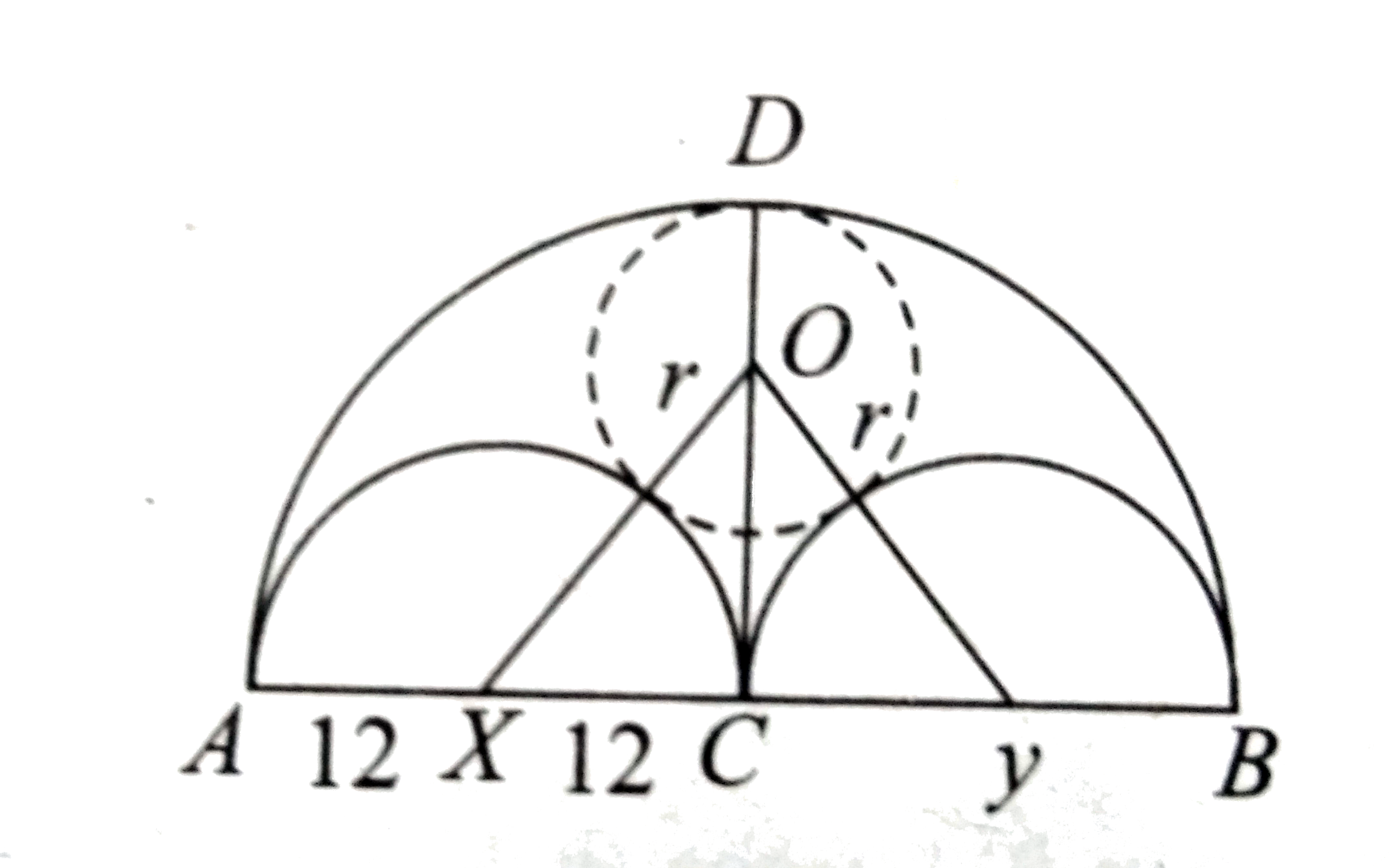
In ΔXCO, we have
OX2+XC2+OC2
⇒(12+r)2=122+(24−r)2
⇒r=8
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type
9 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 4
2 Videos
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
View SolutionLet z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
View SolutionO is the mid-point of line segment AB of length 36 cm. If the semicircles are drawn on AB, OA and OB as diameters, then the radius of the smallest circle which touches all the semicircles is(1) 6 cm (2) 9 cm (3) 12 cm (4) 4 cm.
View SolutionAB is a line segment of length 48 cm and C is its mid-point. If three semicircles are drawn at AB, AC and CB using as diameters, then radius of the circle inscribed in the space enclosed by three semicircles is
View Solutionचित्र में, AB = 36 सेमी. तथा M,AB का मध्यबिन्दु है | AB, AM तथा MB को व्यास लेकर तीन अर्धवृत्त खींचे गए हैं | केन्द्र C वाला एक वृत्त तीनों अर्धवृत्तों को स्पर्श करता है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |

View SolutionModhurima have drawn a semicircle with a diameter AB. A perpendicular is drawn on AB from any point C on AB which intersects the semicircle at the point D. Prove that CD is a mean proportion of AC and BC.
View SolutionAB is a line segment of length 8 cm. Locate a point C on AB such that AC=13CB.
View SolutionIn a triangle with sides, a,b, and c a semicircle toughing the sides AC and CB is inscribed whose diameter lies on AB. Then the radius of the semicricel is
View SolutionIn the adjoining figure , AB is the diameter of a semicircle of maximum possible area . If the radius of the larger circle ( i.e, semicircle ) is r , the area of the inscribed circle is :
View SolutionAB is a line segment of length 48 cm and C is its mid-point. If three semicircles are drawn at AB, AC and CB using as diameters, then radius of the circle inscribed in the space enclosed by three semicircles is
View SolutionAB एक 24 सेमी. लंबी रेखा है जिसका मध्य बिंदु O है । AB, AI और OB का व्यास मानकर रेखा AB के एक ही ओर अर्धवृत्त खींचे गए हैं । एक वृत्त C (O, r) तीनों अर्धवृत्तों को स्पर्श करते हुए खींचा गया है तो त्रिज्या (r) का मान ज्ञात करें ।
View SolutionAB रेखा पर एक बिन्दु C इस प्रकार है कि AC =CB = 2 सेमी। AB, AC और CB पर अर्द्धवृत्त खींचे गए है। यदि एक वृत्त, तीनो अर्द्धवृत्तों से घिरी जगह में इस प्रकार खींचा गया है कि ये तीनो अर्द्धवृत्तों को स्पर्श करता है, तो इस वृत्त का अर्द्धव्यास है।
View SolutionAB रेखा पर एक बिन्दु C इस प्रकार है कि AC = CB = 2 सेमी| AB,AC और CB पर अर्द्धवृत्त खींचे गए हैं। यदि एक वृत्त, तीनों अर्द्धवृत्तों से घिरी जगह में इस प्रकार खींचा गया है कि ये तीनों अर्द्धवृत्तों को स्पर्श करता है, तो इस वृत्त का अर्द्धव्यास है।
View Solution
