Consider two circles S,=x2+y2+8x=0andS2=x2+y2−2x=0. Let ΔPOR be formed by the common tangents to circles S1andS2, Then which of the following hold(s) good?
Incentre of ΔPQR is (1,0)
The equation of radical axis of circles S1 and S2 is y=0
Product of slope of direct common tangents is 169
If transverse common tangent intersects direct common tangents at points A and B, then AB equals 4.
The correct Answer is:A, D
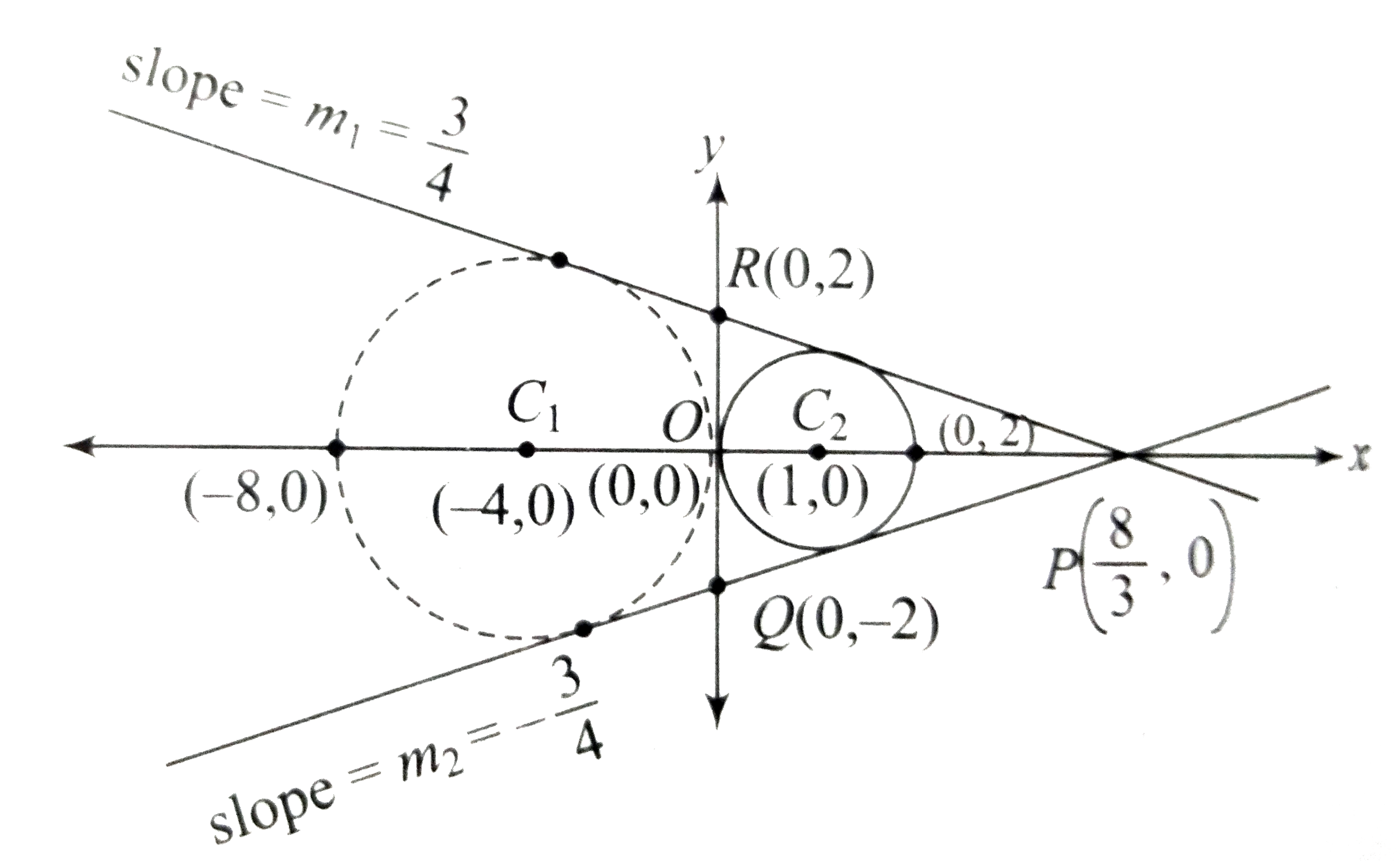
We have S1≡x2+y2+8x=0 with centre (−4,0) and radius =4.
Also, we have S2≡x2+y2−2x=0 with centre (1,0) and radius =1,
Hence, circles S1 and S2 touch each other externally. Also, P(83,0)
(As P divides the line segment joining the centres in a ratio of the radii externally)
Let equation of the direct common tangent by y=m(x−83) By applying condition of tangency, we get
∣∣m−8m3∣∣√1+m2=1
⇒m2=916 or m=±34
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 42videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
COMPLEX NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
The angle between the circles
S: x2+y2−4x+6y+11=0 and S':x2+y2−2x+8y+13=0 isA45∘B90∘C60∘DNone of these - Question 2 - Select One
The common tangents to the circles x2+y2+2x=0 and x2+y2−6x=0 from a triangle which is :
AequilateralBisoscelesCright angledDnone of these - Question 3 - Select One
The point (λ,4) lies outside the circles
S1=x2+y2+10x=0 and
S2=x2+y2−12x+20=0 then λ belong toA(−∞,−8)∪(−2,∞)B(−8,−2)C(−∞,−8)∪(−2,6)∪(6,∞)Dnone
Consider two circles S1=x2+(y−1)2=9 and S2=(x−3)2+(y−1)2=9 , now for these circles match the following :
 View Solution
View SolutionThe common tangents to the circles x2+y2+2x=0andx2+y2−6x=0 form a triangle which is
View SolutionFor the circles S1:x2+y2−4x−6y−12=0 and S2:x2+y2+6x+4y−12=0 and the line L.:x+y=0 (A) L is common tangent of S1 and S2 (B) L is common chord of S1 and S2 (C) L is radical axis of S1 and S2 (D) L is perpendicular to the line joining the cente of S1 & S2
View SolutionThe common tangents to the circles x2+y2+2x=0andx2+y2−6x=0 form a triangle which is
View SolutionIf S≡x2+y2−4x=0,S'≡x2+y2+8x=0 and AB is a direct common tangent to the two circles where A,B are points of contact then find the angle subtended by AB at origin.
View Solution

