If the reflection of the ellipse (x−4)216+(y−3)29=1 in the mirror line x−y−2=0 is k1x2+k2y2−160x−36y+292=0, then k1+k25 is equal to Solution in Bengali
A. 4
B. 5
C. 6
D. 7
The correct Answer is:B
Let (4cosθ+4,3sinθ+3) be any point on the ellipse (x−4)216+(y−3)29=1
Image of (4cosθ+4,3sinθ+3) about the line x−y−2=0 is (h,k), then
h−4cosθ−41=k−3sinθ−3−1=−2(4cosθ−3sinθ−1)2
⇒h=3sinθ+5 and k=4cosθ+2
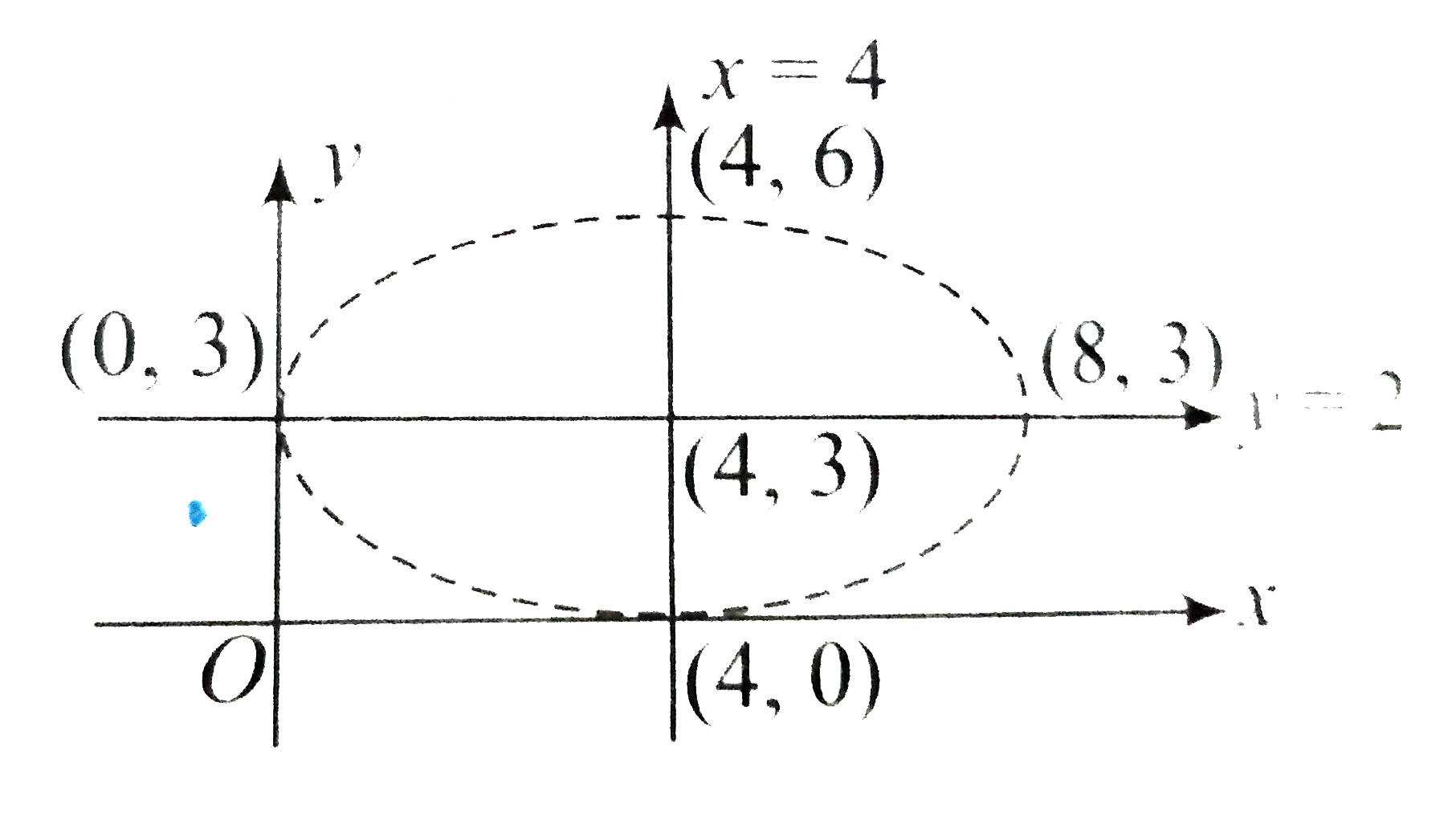
Locus of (h,k) is (x−53)2+(y−24)2=1
⇒16x2+9y2−160x−36y+292=0
⇒k1+k2=25
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - ELLIPSE EXERCISE - Multiple Correct Answers Type6videos
ELLIPSE
- BOOK - CENGAGE PUBLICATIONCHAPTER - DOT PRODUCTEXERCISE - DPP 2.115videos
DOT PRODUCT
- BOOK - CENGAGE PUBLICATIONCHAPTER - EQAUTION OF STRAIGHT LINE AND ITS APPLICATION EXERCISE - DPP 3.213videos
EQAUTION OF STRAIGHT LINE AND ITS APPLICATION
Similar Questions
In triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then
06:43View SolutionLet a,bgt0 and α=ˆia+4ˆjb+bˆk and β=bˆi+aˆtj+1bˆk, then the maximum value of 105+α⋅β is
01:28View SolutionThe ratio in which the plane 2x−1=0 divides the line joining (−2,4,7) and (3,−5,8) is
02:54View SolutionIf the locus of the foot of perpendicular from the centre upon any normal to the hyperbola (x^(2))/(1)-(y^(2))/(2)=1 is (x^(2)+y^(2))(k_(1)y^(2)-k_(2)x^(2))=(k_(1))^(2)x^(2)y^(2), then the value of (k_(1)+k_(2)+k_(3)) is -
09:57View SolutionFind the order of differential equation whose general solution is given by y=(k_(1)+k_(2))tan(x+k_(3))-k_(4)e^(x)+k_(5) where k_(1),k_(2),k_(3),k_(4),k_(5) are arbitrary constants.
03:35View SolutionLet f(x)=(x+1)(x+2)(x+3)(x+4)(x+5) and f'(0) is given as f'(0)=f(0){1+(1)/(k_(1))+(1)/(k_(2))+(1)/(k_(3))+(1)/(k_(4))} then k_(1)+k_(2)+k_(3)-k_(4)=
08:16View SolutionIf the equation on reflection of (x−4)216+(y−3)29=1 about the line x−y−2=0 is 16x2+9y2+k1x−36y+k2=0 then k1+k222 is
03:16View SolutionIf k1 and k2 are roots of x2−5x−24=0, then find the quadratic equation whose roots are −k1 and −k2.
06:36View SolutionIf the reflection of the ellipse (x−4)216+(y−3)29=1 in the mirror line x−y−2=0 is k1x2+k2y2−160x−36y+292=0, then k1+k25 is equal to
02:51View SolutionThe equation x2+k1y2+k2xy=0 represents a pair of perpendicular lines if
06:08View SolutionThe line 3x−y+k=0 touches the circle x2+y2+4x−6y+3=0. If k1,k2(k1<k2) are the two values of k, then the equation of the chord of contact of the point (k1,k2) with respect to the given circle is
06:04View SolutionRepresent the following equations in matrix form:
a1x+b1y+c1z=k1
a2x+b2y+c2z=k2
a3x+b3y+c3z=k302:29View SolutionAn angle of rotation of axes so that [√3x−y+1=0 is transformed as Y=K1 is πK2 then K2K1= where K1in Q,K2in N
07:42View SolutionIf the area bounded by y=x2andy=21+x2 is (K1π−K23) sq. units (where K1,K2∈Z), then the value of (K1+K2) is equal to
07:55View SolutionThe order of the differential equation of the family of curves y=k12k2x+k33x+k4 is (where, k1,k2,k3,k4 are arbitrary constants)
04:28View SolutionIf the reflection of the ellipse (x−4)216+(y−3)29=1 in the mirror line x−y−2=0 is k1x2+k2y2−160x−36y+292=0, then k1+k25 is equal to
02:53View Solution

