Find the locus of the midpoint of the chords of the circle x2+y2=a2 which subtend a right angle at the point (c,0).Solution in Bengali
Let P(h,k) be the midpoint of a chord AB of the circle which subtends a right angle at C(c,0).
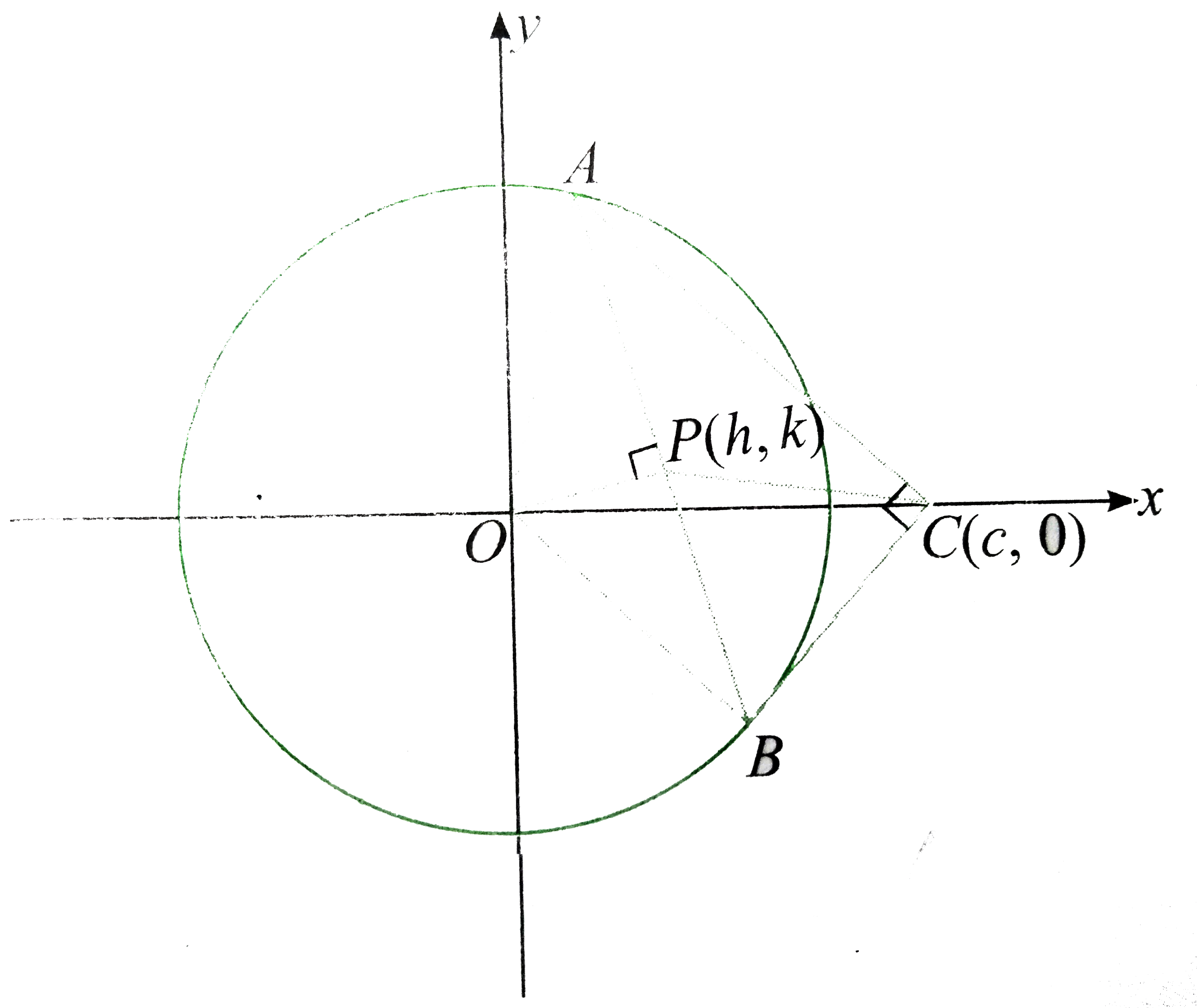
In right angles triangle ACB, we have
PA=PC=PB
PC=√(h−c)2+k2
PB=PA=√OA2−OP2
=√a2−(h2+k2)
Now , PC=PA
∴√(h−c)2+k2=√a2−(h2+k2)
⇒(h−c)2+k2=a2−(h2+k2)
Therefore , the equation of required locus is 2(x2+y2)−2cx+c2−a2=0
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Examples13videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.11videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
The line Ax+By+C=0 cuts the circle x2+y2+ax+by+c=0 at PandQ . The line A′x+B′x+C′=0 cuts the circle x2+y2+a′x+b′y+c′=0 at RandS. If P,Q,R, and S are concyclic, then show that |a−a'b−b'c−c'ABCA'B'C'|=0
03:49View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
10:12View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is03:43View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is02:22View SolutionThe locus of the mid point of a chord of the circle x2+y2=4 which subtends a right angle at the origin is
View SolutionFind the locus of the midpoint of the chords of the circle x2+y2=a2 which subtend a right angle at the point (c,0).
06:25View Solutionfind the locus of mid point of chords of circle x^(2)+y^(2)=25 which subtends right angle at origin
04:11View SolutionThe locus of the mid points of a chord the circle x^(2)+y^(2)=18 which subtends right angle at the origin is
01:14View SolutionLocus of midpoint of chord of circle x2+y2=1 which subtend right angle at (2,−1) is
06:16View SolutionThe locus of the midpoints of chords of the circle x2+y2=1 which subtends a right angle at the origin is
04:24View SolutionThe locus of the midpoint of a chord of the circle x2+y2=4 which subtends a right angle at the origin is
03:07View SolutionThe locus of the mid-points of chords of the circle x2+y2=4, which subtend a right angle at the origin, is:
02:59View SolutionThe locus of the midpoint of chord of the circle x2+y2=1 which subtends a right angle at the origin is
06:43View SolutionFind the locus of the midpoint of the chords of the circle x2+y2−ax−by=0 which subtend a right angle at the point (a2,b2). is
03:07View SolutionFind the locus of the midpoint of the chords of the circle x2+y2=a2 which subtend a right angle at the point (c,0).
03:26View SolutionFind the locus of midpoint of chords of the circle x2+y2=r2 , substending a right angle at the point (a,b)
04:05View Solution

