A circle of radius 1 unit touches the positive x-axis and the positive y-axis at and , respectively. A variable line passing through the origin intersects the circle at two points and . If the area of triangle is maximum when the slope of the line is then find the value of
The equation of the circle is
or (1)
Let the equation of the variable straight line through origin be
(2)
This line intersects the cricle at two points D and E.
Distance of line from point B(0,1) is
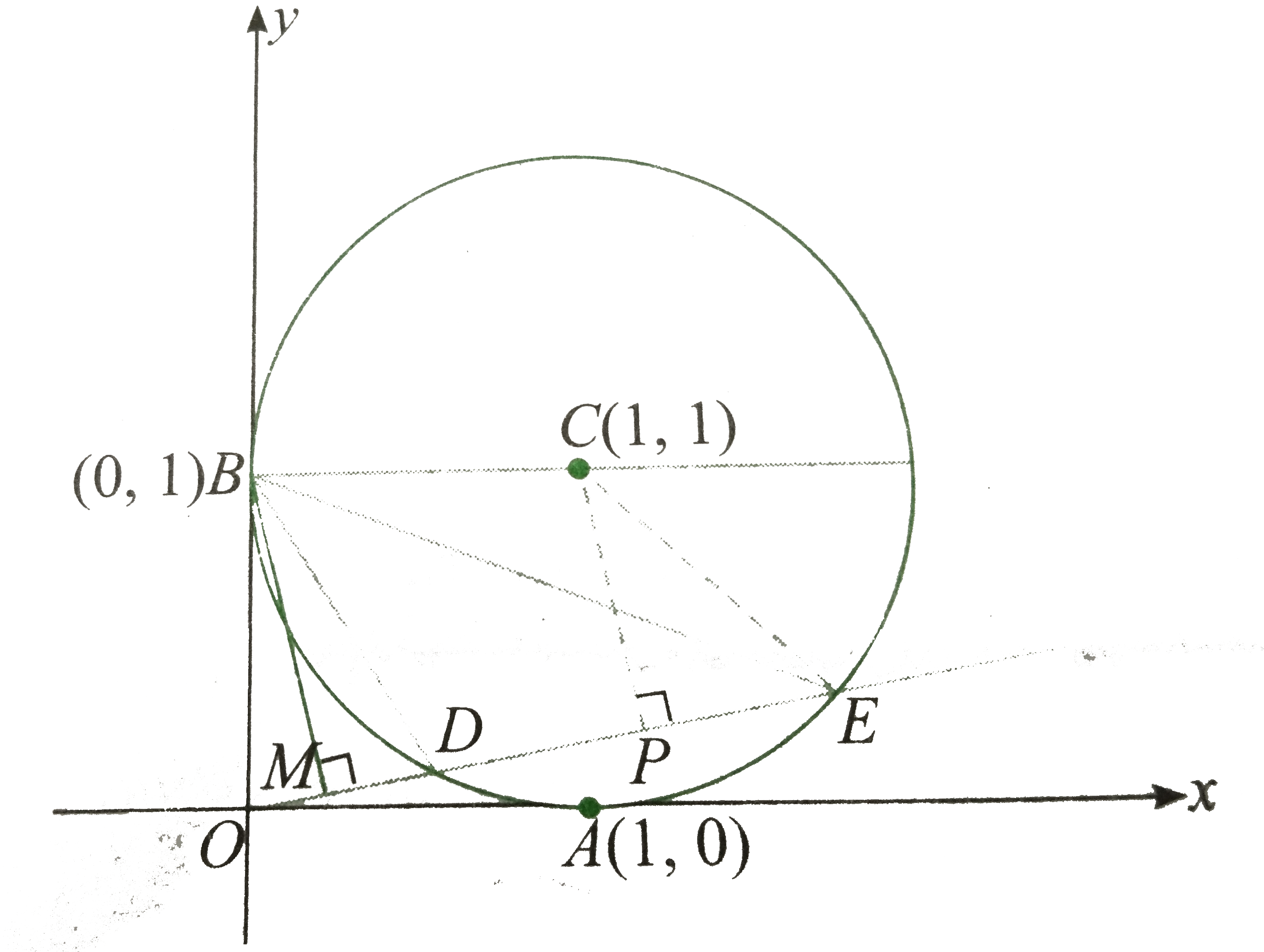
Also,
Area of triangle DEB.
Differentiating w.r.t. m, we get
If , then , whichi is point of maxima.
Therefore, area is maximum if .
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.2
2 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 4
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
A circle of radius 1 unit touches the positive x-axis and the positive y-axis at AandB , respectively. A variable line passing through the origin intersects the circle at two points DandE . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View SolutionIf a line passing through the origin touches the circle (x−4)2+(y+5)2=25 , then find its slope.
View SolutionIf a line passing through the origin touches the circle (x−4)2+(y+5)2=25 , then find its slope.
View SolutionP is a point on positive x-axis, Q is a point on the positive y-axis and 'O' is the origin. If the line passing through P and Q is tangent to the curve y=3−x2 then find the minimum area of the triangle OPQ , is 3 (b) 4 (c) 5 (c) 6
View SolutionCircle with centre C (1, 1) passes through the origin and intersects the x-axis at A and y-axis at B. The area of the part of the circle that lies in the first quadrant is
View SolutionCircle with centre C (1, 1) passes through the origin and intersects the x-axis at A and y-axis at B. The area of the part of the circle that lies in the first quadrant is
View SolutionIf the radius of the circle passing through the origin and touching the line x+y=2 at (1,1) is r units, then the value of 3√2r is
View SolutionA circle C is tangent to the x and y axis in the first quadrant at the points P and Q respectively. BC and AD are parallel tangents to the circle with slope –1. If the points A and B are on the y-axis while C and D are on the x-axis and the area of the figure ABCD is 900 . √2 sq. units then find the radius of the circle.
View SolutionIf a circle passes through the point of intersection of the lines x+y+1=0 and x+λy−3=0 with the coordinate axis, then find the value of λ .
View SolutionA circle passing through (1,1) and (3,3) intersect the positive x -axis at A(a,0) and B(b,0) .Then ab=?
View Solution
