Let A be the centre of the circle x2+y2−2x−4y−20=0 Suppose that the tangents at the points B(1,7) and D(4,-2) on the circle meet at the point C. Find the area of the quadrilateral ABCDSolution in Bengali
The correct Answer is:75 sq. units
The equation of the circle is
x2+y2−2x−4y−20=0
Center ≡(1,2) radius =√1+4+20=5
The equation of tangent at (1,7) is
x.1+y.7−(x+1)−2(y+7)−20=0
or y−7=0 (1)
Similarly, the equation of tangent at (4,-1) is
4x−2y−(x+4)−2(y−2)−20=0
or 3x−4y−20=0 (2)
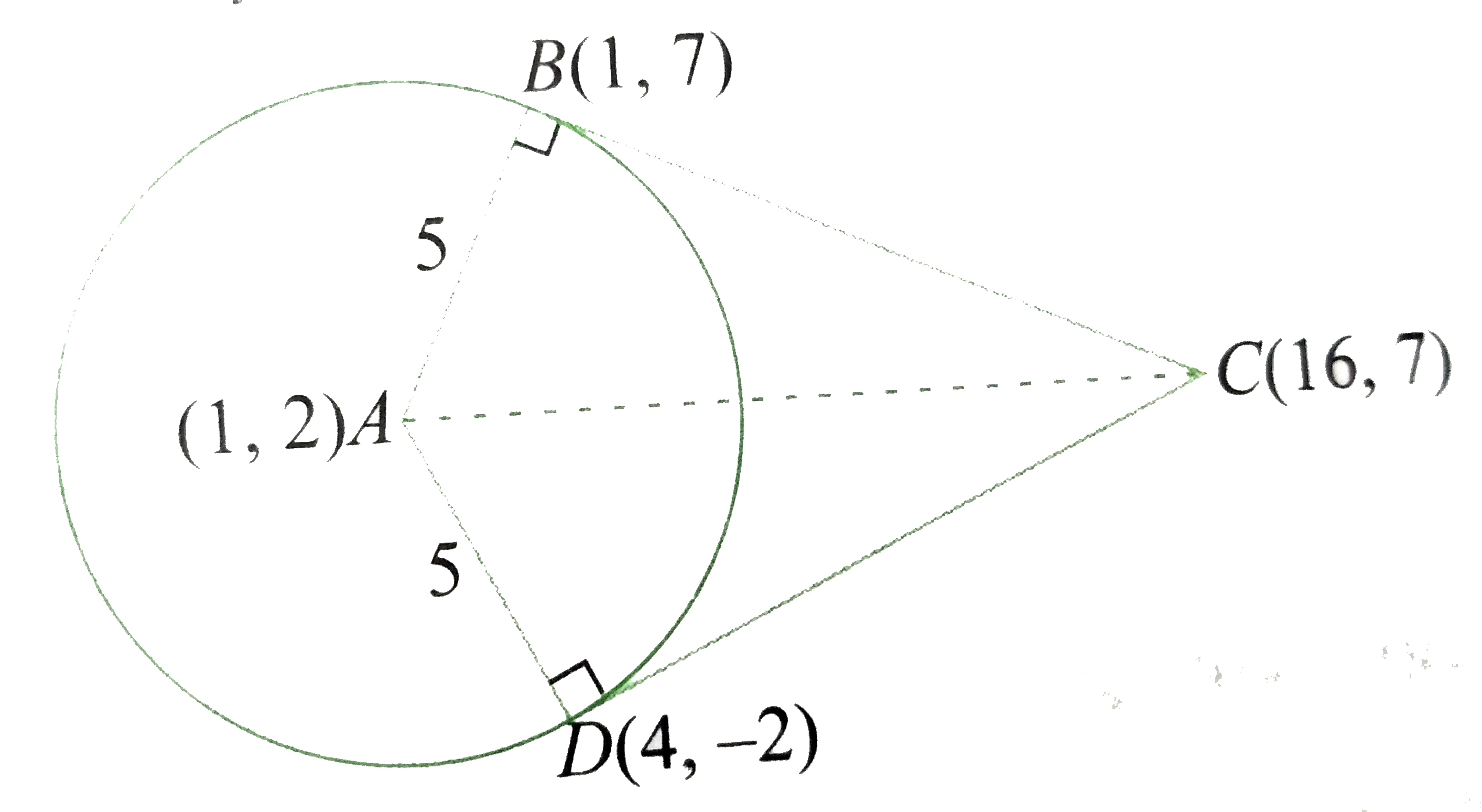
For point C, solving (1) and (2), we get x=16 and y=7 . Therefore, C≡(16,7)
Now, clearly ,
ar(quad. BCDA) =2× ar (ΔABC)
=2×12×AB×BC
=AB×BC
where AB= Radius of circle =5
and BC=15
∴ ar (quad. ABCD) =5×15=75sq. units
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.12
4 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.13
4 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.10
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Number of integral values of λ for which x2+y2+7x+(1−λ)y+5=0 represents the equation of a circle whose radius cannot exceed 5 is
View SolutionProve that the locus of the centroid of the triangle whose vertices are (acost,asint),(bsint,−bcost), and (1,0) , where t is a parameter, is circle.
View SolutionIf one end of the diameter of the circle 2x2+2y2−4x−8y+2=0 is (3,2), then find the other end of the diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View Solution. Let A be the centre of the circle x^(2)+y^(2)-2x-4y-20=0 suppose that x^(2)+y^(2)-2x-4y-20=0 suppose that the tangents at the points B(1,7) and D(4,-2) on the circle meet at the point C. Find the area of the quadrilateral ABCD
View SolutionFrom the point P(16,7), tangents PQ and PR are drawn to the circle x2+y2−2x−4y−20=0 If C is the centre of the circle, then area of quadrilateral PQCR is
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0. Suppose that the tangent at the points B(1,7) and D(4,-2) on the circle meet at the point C. The area of the quadrilateral ABCD is
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0. Let B(1,7) and (4,-2) be two points on the circle such that tangents at B and D meet at C. The area of the quadrilateral ABCD is
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0 .The tangents at the points B(1,7) and C(4,-2) on the circle meet at the point D .If Δ denotes the area of the quadrilateral ABCD,then Δ25 is equal to
View SolutionThe tangent of the circle x2+y2−2x−4y−20=0 at (1,7) meets the y -axis at the point
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0. If the tangents at the points B (1, 7) and D(4,−2) on the circle meet at the point C, then the perimeter of the quadrilateral ABCD is
View Solutionमाना वृत्त x2+y2−2x−4y−20=0 का केन्द्र A है। माना वृत्त पर बिन्दु B(1,7) और D(4,−2) पर खींची गई स्पर्श रेखाएँ C पर मिलती है। चतुर्भुज ABCD का क्षेत्रफल है
View Solutionx2+y2–2x−4y–20=0বৃত্তের কেন্দ্র হল A | মনে কর B(1,7), D(4, -2) ওই বৃত্তের উপরিস্থ দুটি বিন্দু এমন যেB ও D বিন্দুতে অঙ্কিত স্পর্শকদ্বয় c বিন্দুতে ছেদ করে। চতুর্ভুজ ABCD-এর ক্ষেত্রফল হল—
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0 Suppose that the tangents at the points B(1,7) and D(4,-2) on the circle meet at the point C. Find the area of the quadrilateral ABCD
View Solutionमाना वृत्त x2+y2−2x−4y−20=0 का केन्द्र A है। माना वृत्त पर बिन्दु B(1,7) और D(4,−2) पर खींची गई स्पर्श रेखाएँ C पर मिलती है। चतुर्भुज ABCD का क्षेत्रफल है
View Solution
