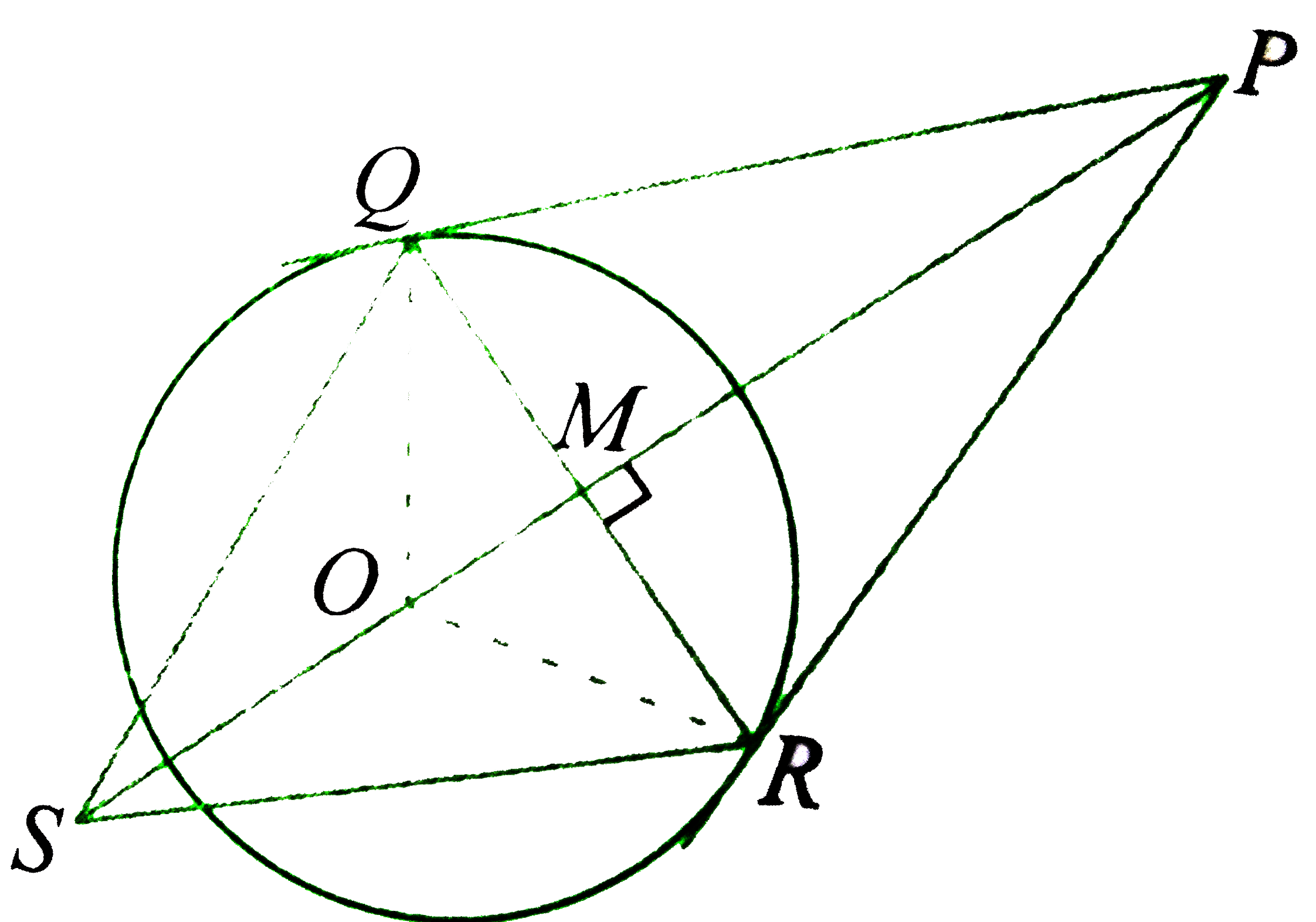
P is a variable point of the line L = 0. Tangents are drawn to the circle x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed. If L=2x+y−6=0, then the locus of circumcetre of △PQR is -Solution in Bengali
2x−y=4
2x+y=3
x−2y=4
x+2y=3
The correct Answer is:2
PQ=PR, i.e., paralleleogram PQSR is a rhombus. Therefore,
Midpoint of QR= Midpoint of PS and QR⊥PS
Therefore , S is the mirror image of P in QR
L≡2x+y−6
Let P≡(k,6−2k) .
∠PQO=∠PRO=π2
Therefore, OP is the diameter of circumsircle PQR. Then the center is (k/2,3−k) . So,
x=k2 or k=2x and y=3−k
Therefore, the required locus is 2x+y=3
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE7videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE21videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
Match the following lists.
 09:18View Solution
09:18View SolutionLet the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2+gx+fy+7=0 , then the value of |f+g| is__________
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is04:29View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is09:19View SolutionP is a variable point of the line L=0. Tangents are drawn to the circle x^(2)+y^(2)=4 from P is touch it at Q and R .The parallelogram PQSR is completed.If L=2x+y-6=0, then the locus of circumcetre of /_PQR is.
03:30View SolutionP is a variable point on the line L=0 . Tangents are drawn to the circles x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed.
If P≡(6,8), then the area of ΔQRS is07:32View SolutionP is a variable point on the line L=0 . Tangents are drawn to the circles x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed.
If P≡(3,4), then the coordinates of S are01:59View SolutionP is a variable point on the line L=0. Tangents are drawn to the circle x2+y2=4 from P to touch it at Q and R. The parallelogran PQSR is completed.
If P-=(6,8) then area of ΔQRS is 19225√λ sq units. The value of λ is02:28View SolutionP is a variable point on the line L=0. Tangents are drawn to the circle x2+y2=4 from P to touch it at Q and R. The parallelogran PQSR is completed.
If p-=(3,4), then the coordinates of S are05:26View SolutionThe variable point P at the line L = 0 is the circle from the point P x^(2) + y^(2) = 4 The tangent lines drawn at Q touch the circle at Q and R. PQSR is a parallelogram. If L = 2x + y = 6, then Delta PQR Is the locus of the circumcentre of
04:26View SolutionThe variable point P at the line L = 0 is the circle from the point P x^(2) + y^(2) = 4 The tangent lines drawn at Q touch the circle at Q and R. PQSR is a parallelogram. If P -= (2, 3) If so Delta QRS Is the center of the circumcircle of
07:32View SolutionP is a variable point of the line L = 0. Tangents are drawn to the circle x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed. If L=2x+y−6=0, then the locus of circumcetre of △PQR is -
04:30View SolutionP is a variable point on the line L=0 . Tangents are drawn to the circles x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed.
If P≡(6,8), then the area of ΔQRS is04:26View SolutionP is a variable point on the line L=0 . Tangents are drawn to the circles x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed.
If P≡(3,4), then the coordinates of S are07:32View SolutionA variable point P is located at L = 0. Circle from point P x^(2) + y^(2) = 4 But tangent lines are drawn, which touch the circle at the points Q and R. The parallelogram PQSR becomes complete. Day! = 2x + y - 6 = 0, then DeltaPOR Is the locus of the circumcentre of
04:26View Solution

