With a given point and line as focus and directrix, a series of ellipses are described. The locus of the extremities of their minor axis is an ellipse (b) a parabola a hyperbola (d) none of theseSolution in Bengali
an ellipse
a parabola
a hyperbola
none of these
Let S be the given focus and ZM be the given directrix. Then,
SZ=ae−ae
=ae(1−e2)
=b2aek (say)
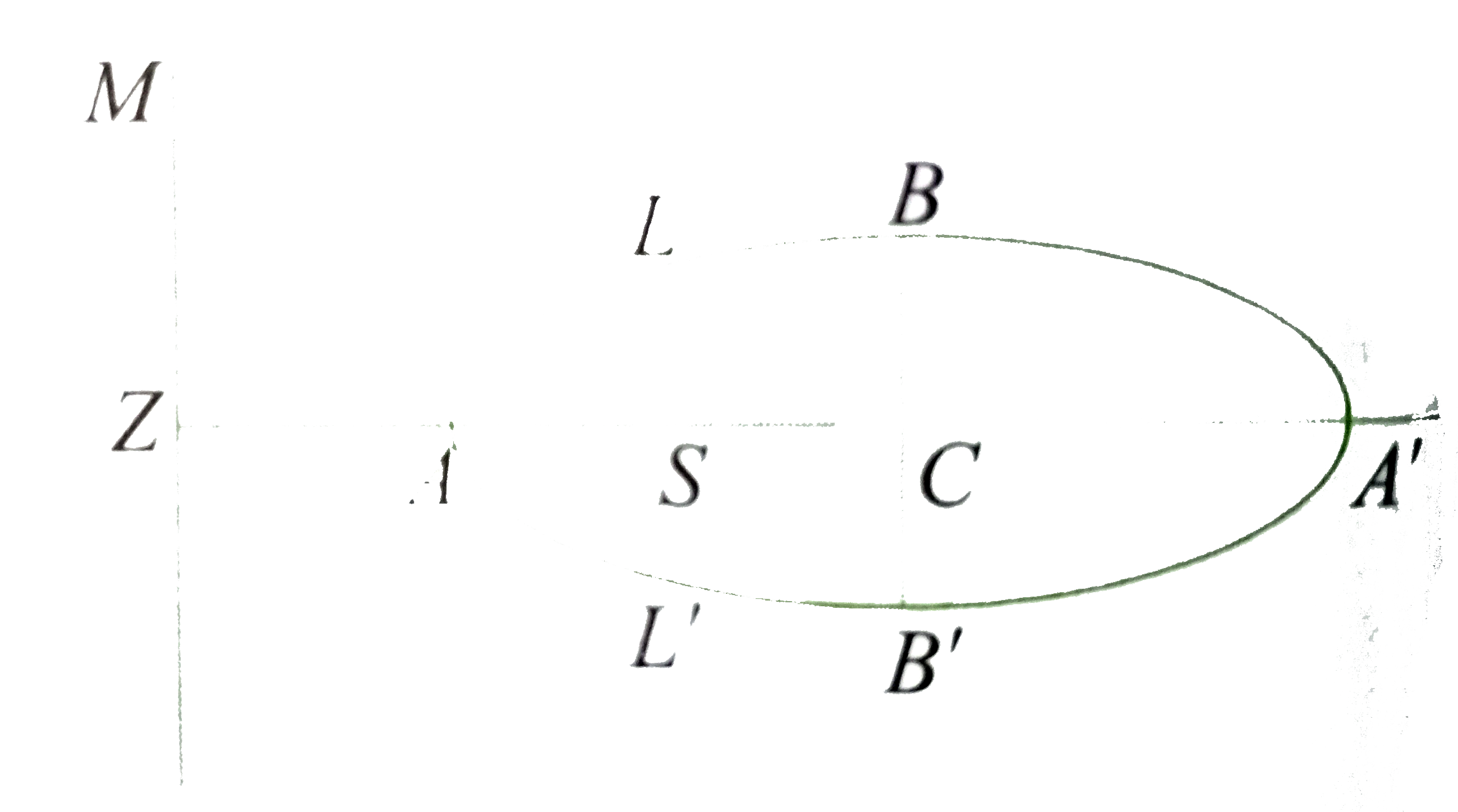
Now, take SC as the x-axis and LS'L as the y-axis . Let (x,y() be the coordinaters of B with respect to these axes. Then , x=SC=ae and y =CB=b b. Hence,
x2a2=b2ae=SZ
Which is constan.
Therefore, y2=kx is the required locus which is a parabola.
Similar Questions
An ellipse and a hyperbola are confocal (have the same focus) and the conjugate axis of the hyperbola is equal to the minor axis of the ellipse. If e1ande2 are the eccentricities of the ellipse and the hyperbola, respectively, then prove that 1e12+1e22=2 .
02:20View SolutionWith a given point and line as focus and directrix, a series of ellipses are described. The locus of the extremities of their minor axis is an ellipse (b) a parabola a hyperbola (d) none of these
02:57View SolutionIn an ellipse, if the lines joining focus to the extremities of the minor axis form an equilateral triangle with the minor axis, then the eccentricity of the ellipse is
04:36View SolutionIn an ellipse if the lines joining focus to the extremities of the minor axis from an equilateral triangle with the minor axis then find the eccentricity of the ellipse.
06:07View SolutionVariable ellipses are drawn with x=−4 as a directrix and origin as corresponding foci. The locus of extremities of minor axes of these ellipses is:
06:45View SolutionA parabola is drawn to pass through AandB the ends of a diameter of a given circle of radius a and to have as directrix a tangent to a concentric circle of radius b, the axes being AB and a perpendicular diameter. The locus of the focus of the parabola is a conic which is : (A) a parabola (B) an ellipse (C) a hyperbola which is not a rectangular hyperbola (D) a rectangular hyperbola
06:29View SolutionWith a given point and line as focus and directrix, a series of ellipses are described. The locus of the extremities of their minor axis is an (a)ellipse (b)a parabola (c)a hyperbola (d)none of these
04:46View SolutionAn ellipse and a hyperbola are confocal (have the same focus) and the conjugate axis of the hyperbola is equal to the minor axis of the ellipse. If e1ande2 are the eccentricities of the ellipse and the hyperbola, respectively, then prove that 1e12+1e22=2 .
09:20View Solution

