The area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latus rectum to the ellipse x29+y25=1 is (a) 274 (b) 18 (c) 272 (d) 27 Solution in Bengali
27/4 sq units
9 sq. units
27/2 sq .units
27 sq.units
The given ellipse is
x29+y25=1
Then , a2=9,b2=5. Therefore,
e=√1−59=23
The equation of tangent at L is 2x9+y3=1
The tangent meets rthe x-axis at A(9/2,0) and the y-axis at B(0,3) . Therefore,
Area of ΔOAB=12×92×3=274
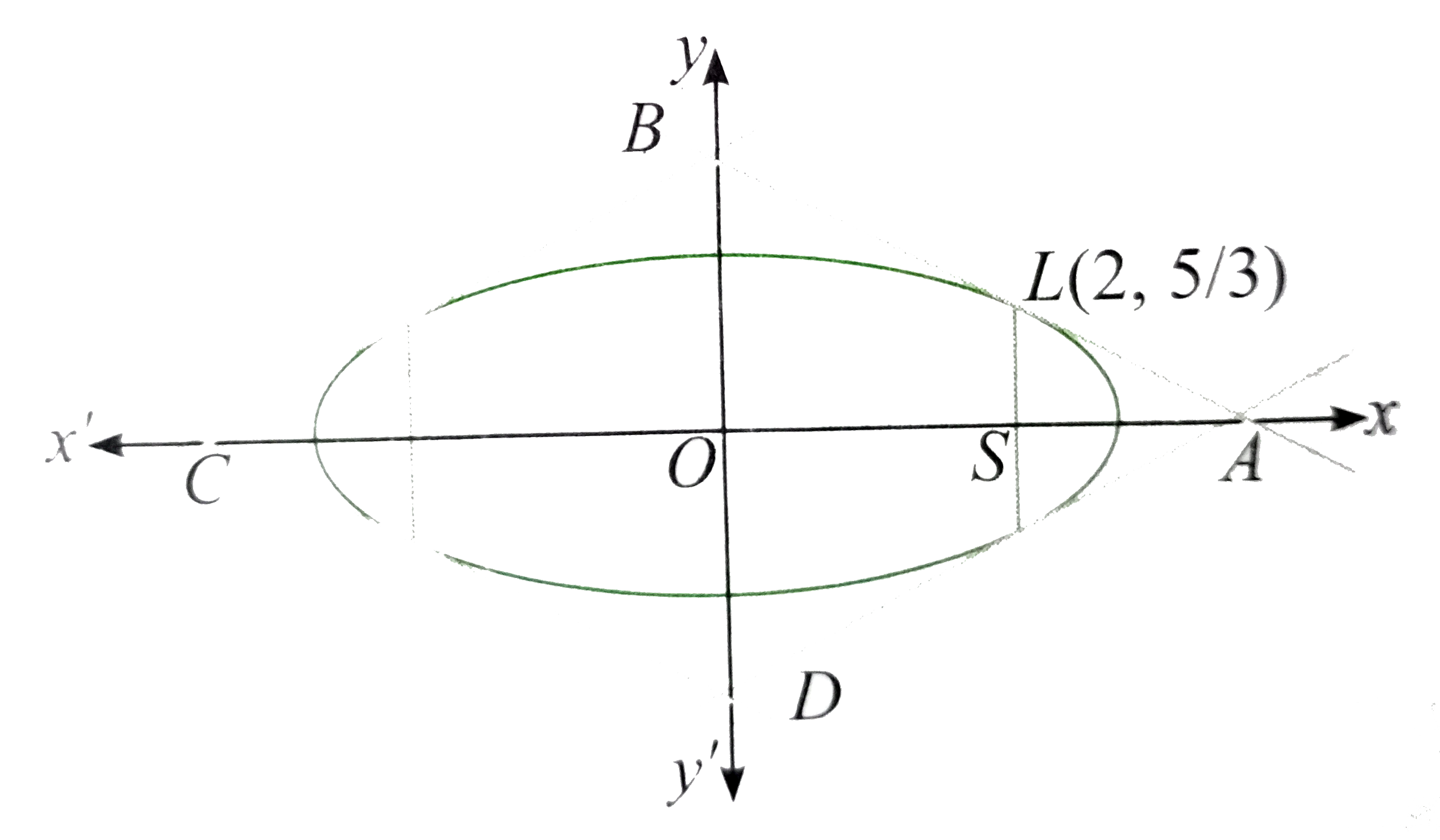
By symmetry,
Area of quadrilateral =4×(Area of ΔOAB)
=4×274=27 sq. units
Similar Questions
The area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latus rectum to the ellipse x29+y25=1 is (a) 274 (b) 18 (c) 272 (d) 27
06:09View SolutionThe area of the quadrilateral formed by the tangents drawn at extreme points of latus reactum of an ellipse x29+y25=1 is …Sq. units .
View SolutionTangents are drawn to the ellipse x29+y25=1 at the end of latus rectum. Find the area of quadrilateral so formed
07:22View SolutionArea of the quadrilateral formed by the tangents at the ends of latus rectum of x225+y216=1 is (in sq. units)
04:39View SolutionThe area of the quadrilateral formed by the tangents at the end points of latus rectum to the ellipse x29+y25=1 is
06:39View SolutionThe area (in sq. units) of the triangle formed by the latus rectum and the tangents at the end points of the latus rectum of x216−y29=1 is equal to
04:25View SolutionThe area of the quadrilateral formed by the tangents at the endpoint of the latus rectum to the ellipse (x^2)/9+(y^2)/5=1 is (A) 27/4 sq. unit (B) 9 sq. units (C) 27/2 sq. unit (D) 27 sq. unit
06:22View SolutionThe area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latus rectum to the ellipse x29+y25=1 is (a) 274 (b) 18 (c) 272 (d) 27
04:27View Solution

