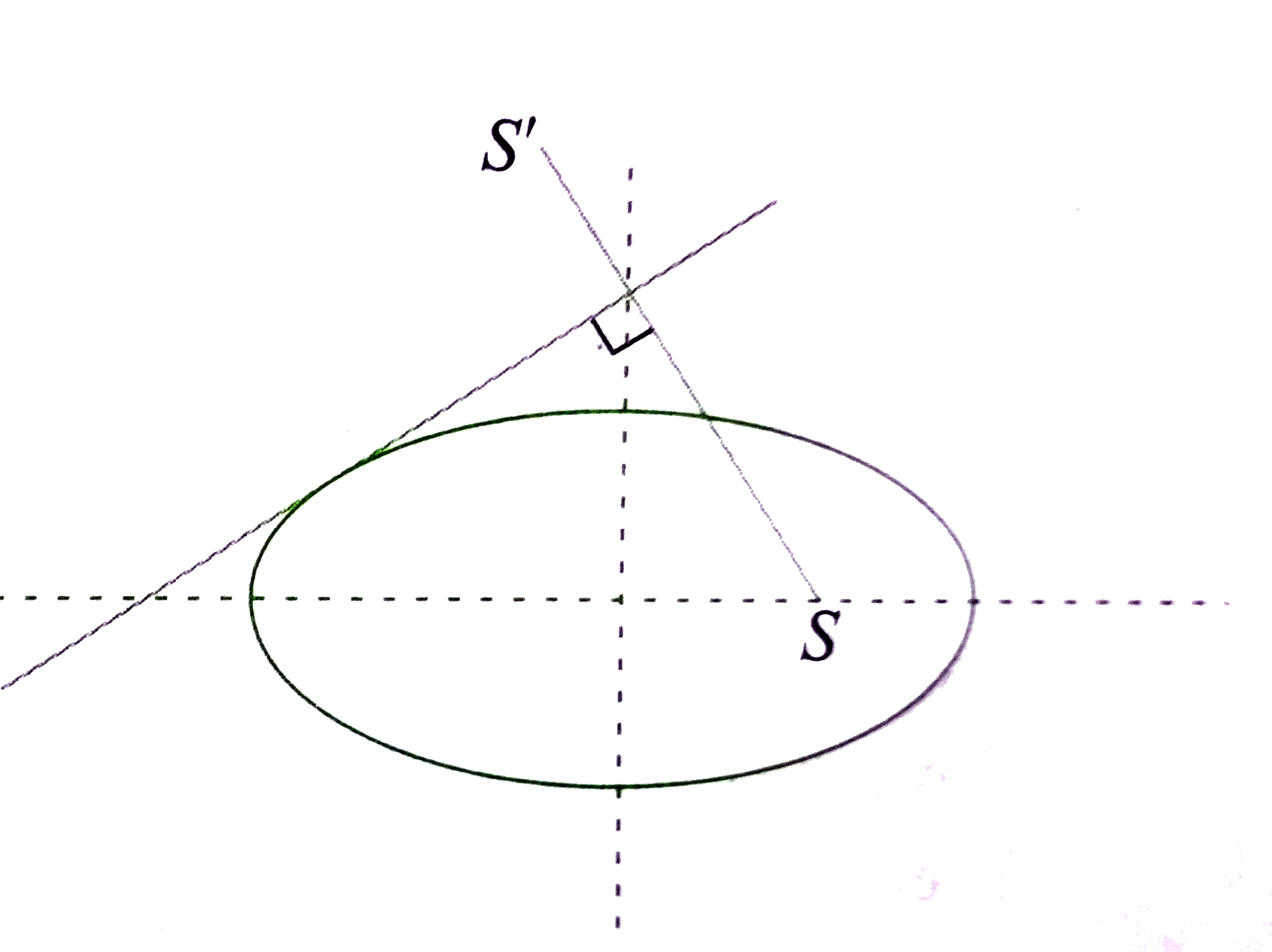
The locus of the image of the focus of the ellipse x225+y29−1,(a>b), with respect to any of the tangents to the ellipse is (x+4)2+y2=100 (b) (x+2)2+y2=50 (x−4)2+y2=100 (d) (x+2)2+y2=50Solution in Bengali
(x+4)2+y2=100
(x+2)2+y2=50
(x−4)2+y2=100
(x−2)2+y2=50
Let S''(h,k)be the image.
SS'' cuts a tangents at a point which lies on the auxiliary circle of the ellipse. Therefore,
(h±42)+k24=25
Hence the locus is (x±4)+y2=100
Similar Questions
The locus of the poles of the tangents to the ellipse x2a2+y2b2=1 w.r.t. the circle x2+y2=a2 is:
04:29View SolutionThe locus of foot of perpendicular from focus of ellipse x2a2+y2b2=1 to its tangents is
08:35View SolutionThe minimum length of intercept on any tangent to the ellipse x24+y29=1 cut by the circle x2+y2=25 is :
View SolutionThe locus of the image of the focus of the ellipse x225+y29=1,(a>b), with respect to any of the tangents to the ellipse is: (a) (x+4)2+y2=100 (b) (x+2)2+y2=50 (c) (x−4)2+y2=100 (d) (x+2)2+y2=50
03:11View SolutionThe minimum length of intercept on any tangent to the ellipse x24+y29=1 cut by the circle x2+y2=25 is :
04:21View SolutionThe locus of the poles of the tangents to the ellipse x2a2+y2b2=1 w.r.t. the circle x2+y2=a2 is: (a) parabola (b) ellipse (c) hyperbola (d) circle
04:50View SolutionThe locus of poles of tangents to the ellipse x2a2+y2b2=1 with respect to concentric ellipse x2α2+y2β2=1 is
03:04View SolutionThe locus of the poles of tangents to the director circle of the ellipse x2a2+y2b2=1 with respect to the ellipse x2a2+y2b2=1 is
04:45View Solution

