The normal at a point P on the ellipse x2+4y2=16 meets the x-axis at Q. If M is the midpoint of the line segment PQ, then the locus of M intersects the latus rectums of the given ellipse at points. ⎛⎜ ⎜⎝±(3√5)2±27⎞⎟ ⎟⎠ (b) ⎛⎜ ⎜⎝±(3√5)2±√197⎞⎟ ⎟⎠ (±2√3,±17) (d) (±2√3±4√37)Solution in Bengali
(±3√5/2,±2/7)
(±3√5/2,±√19/7)
±2√3,±17)
(±2√3,±4√3/7)
Given ellipse is x216+y24=1. Normal at P(4cosϕ,2sinϕ),
given by 4xsecϕ−2ycosecϕ=12
It meets x-axist at
Let M≡(α,β)
be the point of PQ.
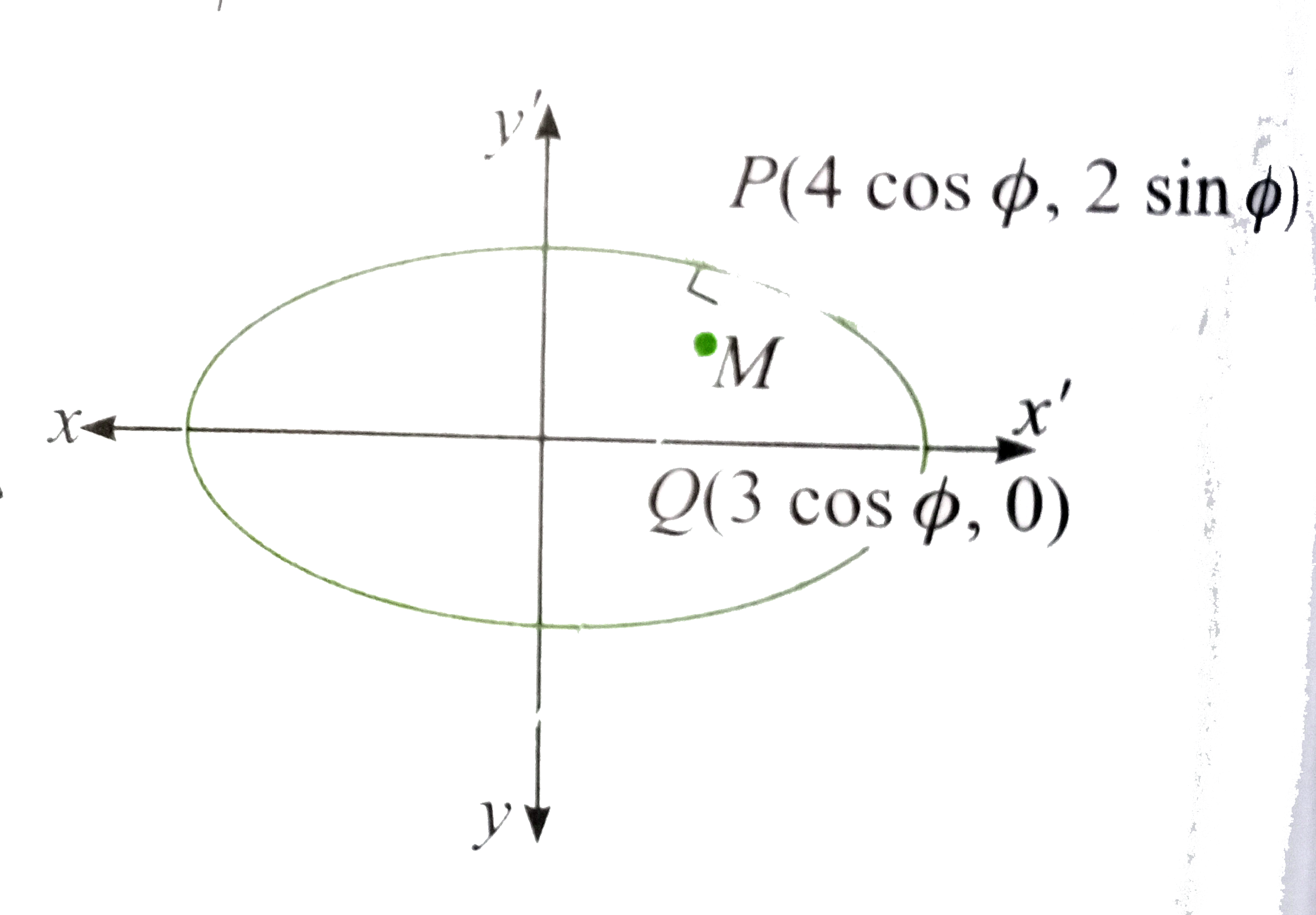
∴α=3cosϕ+4cosϕ2
=72cosϕ
or cosϕ=27α
Using cos2ϕ+sin2ϕ=1, we have
449α2+β2=1
or 449x2+y2=1
Now, the rectum lines of given ellipse are x=±2√3
Solving (1) and (2), we have
4849+y2=1
ory=±17
The points of intersection are (±2√3,±1/7)
Similar Questions
The normal at a point P on the ellipse x2+4y2=16 meets the x-axis at Q. If M is the midpoint of the line segment PQ, then the locus of M intersects the latus rectums of the given ellipse at points. (a)⎛⎜ ⎜⎝±(3√5)2±27⎞⎟ ⎟⎠ (b) ⎛⎜ ⎜⎝±(3√5)2±√197⎞⎟ ⎟⎠ (c)(±2√3,±17) (d) (±2√3±4√37)
05:24View SolutionIf tangents PQ and PR are drawn from a point on the circle x2+y2=25 to the ellipse x216+y2b2=1,(b<4), so that the fourth vertex S of parallelogram PQSR lies on the circumcircle of triangle PQR , then the eccentricity of the ellipse is
(a)√54
(b) √74
(c) √72
(d) √5304:55View SolutionSimplify each of the following by rationalising the denominator: 7+3√57−3√5 (ii) 2 √3− √52√2+ 3√3
06:26View SolutionFor the ellipse x2+4y2=9 a. the eccentricity is 1/2 b. the latus rectum is 3/2 c. a focus is (3√3,0) d. a directrix is x=−2√3
03:21View SolutionIf we reduce 3x+3y+7=0 to the form xcosα+ysinα=p, then the value of p is 72√3 (b) 73 (c) 3√72 (d) 73√2
03:35View SolutionIf pair of tangents are drawn to the ellipse x216+y29=1 from a point P so that the tangents are at right angles to each other, then the possible coordinates of the point P is/are (A) (3√2,√7) (B) (5,0) (C) (3,4) (D) (2√5,√5)
08:51View SolutionThe normal at a point P on the ellipse x^2+4y^2=16 meets the x-axis at Qdot If M is the midpoint of the line segment P Q , then the locus of M intersects the latus rectums of the given ellipse at points. (a) (+-((3sqrt(5)))/2+-2/7) (b) (+-((3sqrt(5)))/2+-(sqrt(19))/7) (c) (+-2sqrt(3),+-1/7) (d) (+-2sqrt(3)+-(4sqrt(3))/7)
05:59View SolutionThe normal at a point P on the ellipse x2+4y2=16 meets the x-axis at Q. If M is the midpoint of the line segment PQ, then the locus of M intersects the latus rectums of the given ellipse at points. (a)⎛⎜ ⎜⎝±(3√5)2±27⎞⎟ ⎟⎠ (b) ⎛⎜ ⎜⎝±(3√5)2±√197⎞⎟ ⎟⎠ (c)(±2√3,±17) (d) (±2√3±4√37)
06:01View Solution

