Question

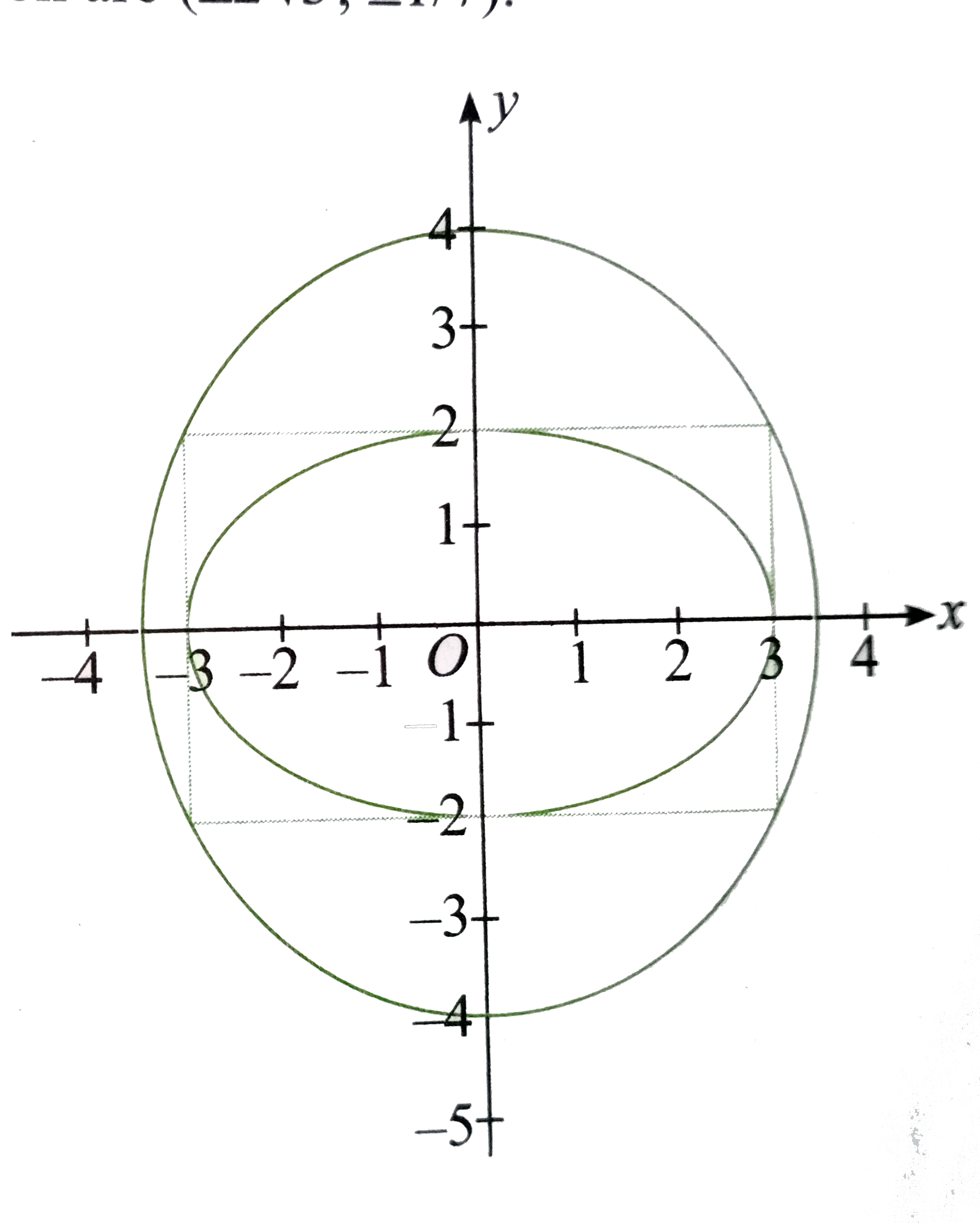
The ellipse $E_1:\frac{x^2}{9}+\frac{y^2}{4}=1$
is inscribed in a rectangle $R$
whose sides are parallel to the coordinate axes. Another ellipse $E_2$
passing through the point (0, 4) circumscribes the rectangle $R\stackrel{.}{}$
The eccentricity of the ellipse $E_2$
is
$\frac{\sqrt{2}}{2}$
(b) $\frac{\sqrt{3}}{2}$
(c) $\frac{1}{2}$
(d) $\frac{3}{4}$

Options

A. `sqrt(2)//2`
B. `sqrt(3)//2`
C. `1//2`
D. `3//4`

Explanation

Let the ellipse be
`(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
as it passing through (0,4) and (3,2). So,
`b^(2)=16 and (9)/(a^(2))+(4)+(16)=1`
or `a^(2)=12` ltbr So, `12=16(1-e^(2))`
or `e=(1)/(2)`