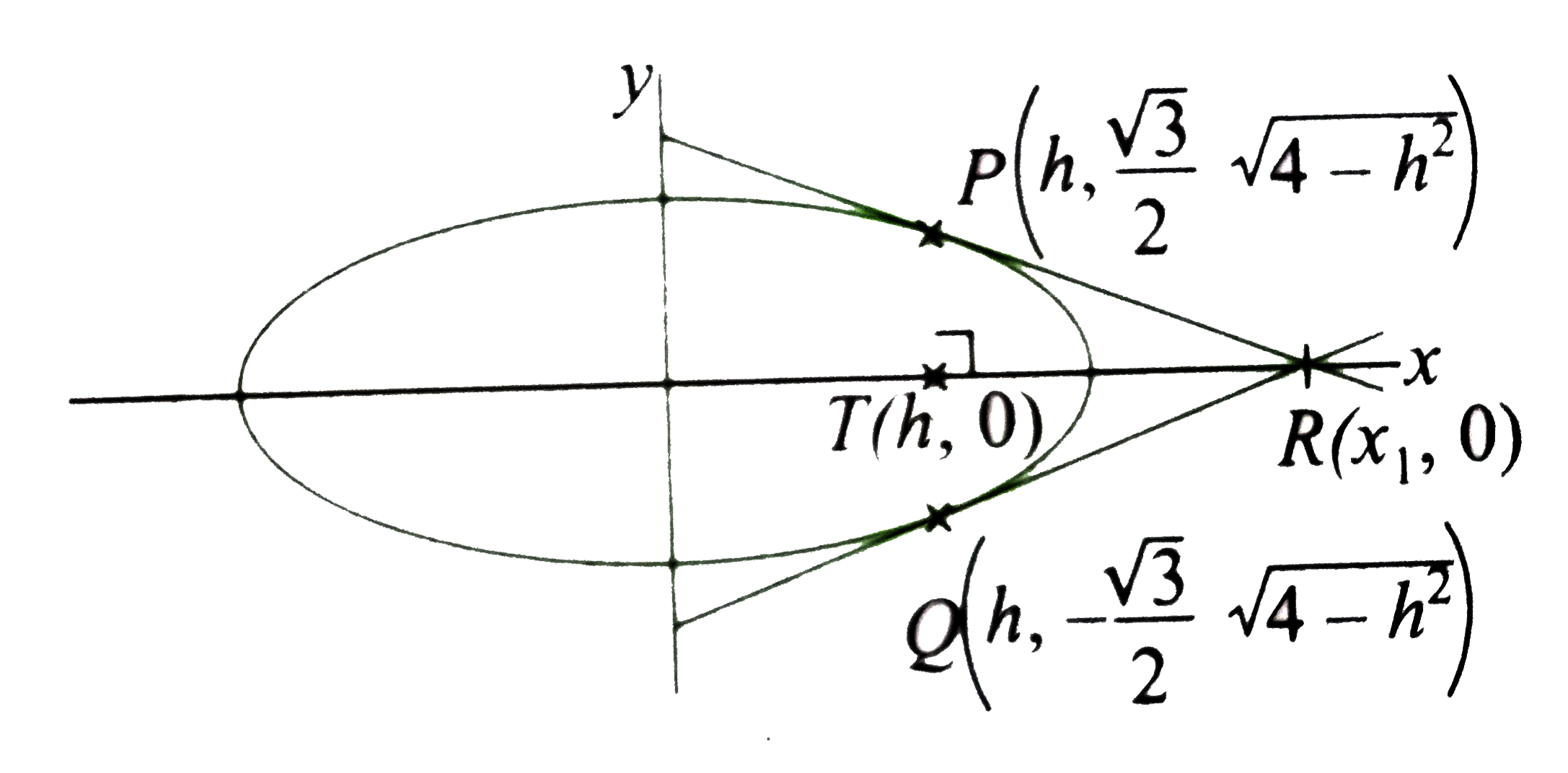
A vertical line passing through the point (h,0) intersects the ellipse x24+y23=1 at the points P and Q.Let the tangents to the ellipse at P and Q meet at R. If Δ(h) Area of triangle ΔPQR, and Δ1=max12≤h≤1Δ(h) and Δ2=min12≤h≤1Δ(h) Then 8√5Δ1−8Δ2
x24+y23=1
∴Y=√32√4−h2atx=h
Let R(x1,0)
PQ, is the chord of contant So, xx14=1
or x=4x1
Which is the euation of PQ. At x=h
xx1=horx1=4h
Δ(h)=Area ofΔPQR=12×PQ×RT
=12×2√32√4−h2×(x1−h)=√32h(4−h2)3/2
Clearly, Δh=45√58ath=12
and Δ2 Minimum of Δ(h)=92ath=1
So, 8√5Δ1−8Δ2=8√5×45√58−×92=45−36=9
Similar Questions
A vertical line passing through the point (h, 0) intersects the ellipse x24+y23=1 at the point P and Q. Let the tangets to the ellipse at P and Q meet at the point R. If △(h)= area of the triangle PQR,
△1= max △(h) and △2= max △(h) 12≤h≤1 12≤h≤1
Then 8√5△1−8△2=View SolutionIf 3x+4y=12 intersect the ellipse x225+y216=1 at P and Q , then point of intersection of tangents at P and Q.
View Solution
Knowledge Check
- Question 1 - Select One
Lines x+y=1and3y=x+3 intersect the ellipse x2+9y2=9 at the points P,Q,R. the area of the triangles PQR is
A365B185C95D15 - Question 2 - Select One
Tangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at points A and B. The orthocenter of the △PAB is
A(5,87)B(75,258)C(115,85)D(825,75) - Question 3 - Select One
Tangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at points A and B. The orthocentre of ΔPAB, is
A(5,87)B(75,258)C(115,85)D(825,75)
If 3x+4y=12 intersect the ellipse x225+y216=1 at P and Q , then point of intersection of tangents at P and Q.
View SolutionA variable tangent to the circle x2+y2=1 intersects the ellipse x24+y22=1 at point P and Q. The lous of the point of the intersection of tangents to the ellipse at P and Q is another ellipse. Then find its eccentricity.
View SolutionA variable tangent to the circle x2+y2=1 intersects the ellipse x24+y22=1 at point P and Q. The lous of the point of the intersection of tangents to the ellipse at P and Q is another ellipse. Then find its eccentricity.
View SolutionNormal at a point P(a,-2a) intersects the parabola y2=4ax at point Q.If the tangents at P and Q meet at point R,if the area of triangle PQR is 4a2(1+m2)3mλ.Then find λ
View Solutionif a variable tangent of the circle x2+y2=1 intersects the ellipse x2+2y2=4 at P and Q. then the locus of the points of intersection of the tangents at P and Q is
View Solution

