Suppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is Solution in Bengali
The correct Answer is:9
According to question →s=4→p+3→q+5→rand→s=x(−→p+→q+→r)+y(→p−→q+→r)+z(−→p−→q+→r)
∴−x+y−z=4 (1)
x−y−z=3 (2)
x+y+z=5 (3)
Adding (1) and (2), we get
z=−72
Adding (2) and (3), we get
x=4
Adding (1) and (3), we get
y=9/2
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - INTRODUCTION TO VECTORS EXERCISE - ARCHIVES SUBJECTIVE TYPE9videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INTRODUCTION TO VECTORS EXERCISE - FILL IN THE BLANKS2videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE3videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INTEGRALSEXERCISE - All Questions762videos
INTEGRALS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions541videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Find the all the values of lamda such that (x,y,z)≠(0,0,0)and x(ˆi+ˆj+3ˆk)+y(3ˆi−3ˆj+ˆk)+z(−4ˆi+5ˆj)=λ(xˆi+yˆj+zˆk)
01:45View SolutionIf a,b, and c are all different and if
∣∣ ∣ ∣∣aa21+a3bb21+b3cc21+c3∣∣ ∣ ∣∣=0 Prove that abc =-1.03:32View SolutionRefer to the following diagram :

Column IColumn IIa.Collinear vectorsp.→ab.Coinitial vectorsq.→bc.Equal vectorsr.→cd.Unlike vectors (same initial point)s.→d04:11View SolutionIf ∫dxx2+ax+1=f(g(x))+c, then f(x) is inverse trigonometric function for |a|>2 f(x) is logarithmic function for |a|<2 g(x) is quadratic function for |a|>2 g(x) is rational function for |a|<2
04:28View SolutionFind x satisfying [tanx]+[cotx]=2, where [.] represents the greatest integer function.
View SolutionIf vecP+vecQ=vecR and vecP-vecQ=vecS , prove that vecR^2+vecS^2=2(vecP^2+vecQ^2)
03:27View SolutionIf vecP+vecQ=vecR" & "vecR is perpendicular to vecP . define angle between vecP" & "vecQ" if " vec|P|=vec|R|-
02:22View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:
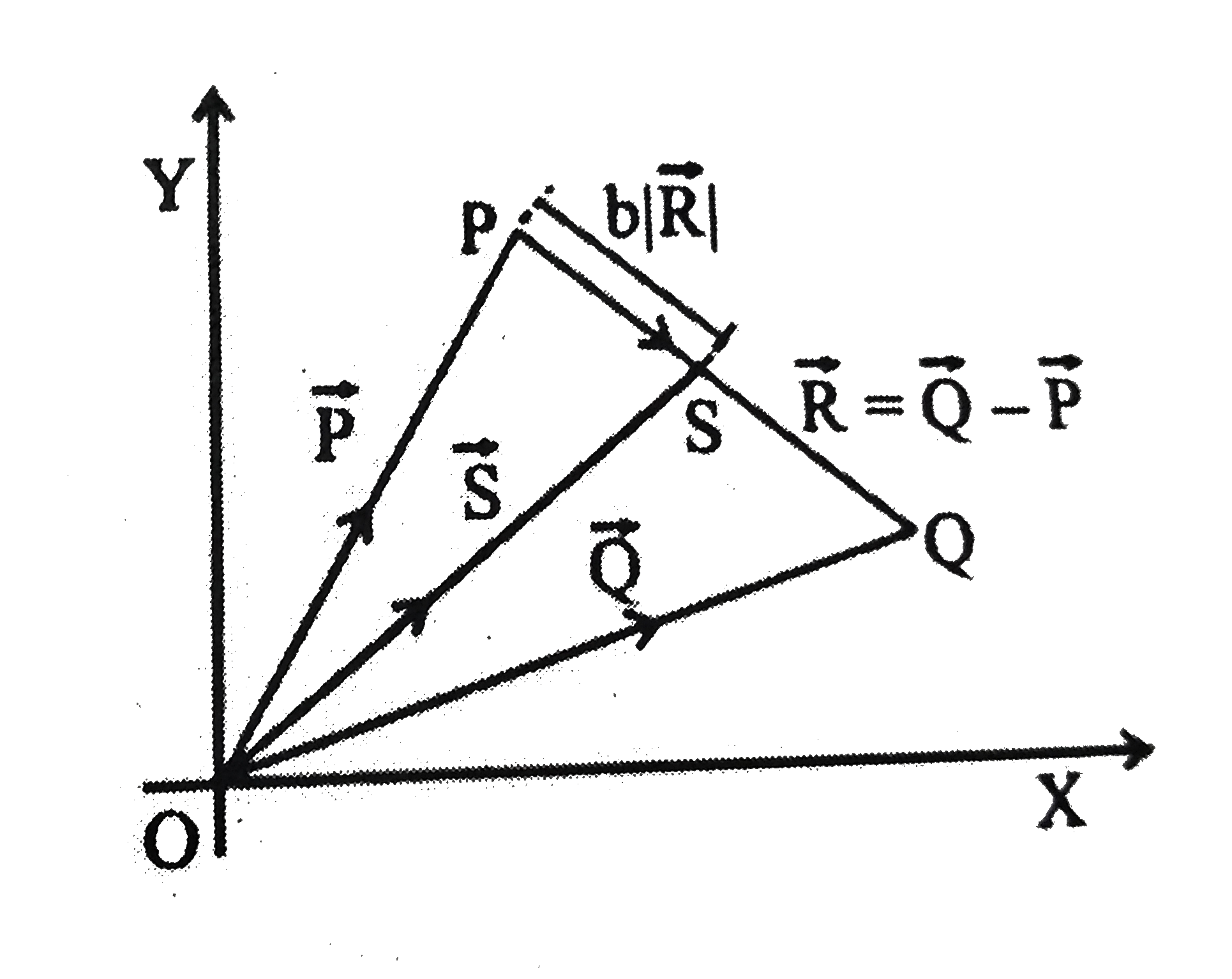 08:21View Solution
08:21View SolutionSuppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is
14:24View SolutionSuppose that →p,→qand→r are three non-coplanar vectors in R3. Let the components of a vectors →s along →p,→qand→r be 4, 3 and 5, respectively. If the components of this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x,yandz, respectively, then the value of 2x+y+z is
03:06View SolutionLet →qand→r be non - collinear vectors, If →p is a vector such that →p.(→q+→r)=4and→p×(→q×→r)=(x2−2x+9)→q then +(siny)→r
(x, y) lies on the line03:14View SolutionFor three vectors vecP, vecQ and vecR, vecP+vecQ=vecR and P+Q=R Then prove that vecP and vecQ are parallel to each other.
View SolutionR3 -এর মধ্যে তিনটি অসমতলীয় ভেক্টর হল →p,→q ও→r। মনে করো, →p,→q ও →rভেক্টর তিনটির অভিমুখে →s-ভেক্টরের ভেক্টর উপাংশ 4,3 এবং 5। যদি (−→p+→q+→r),(→p−→q+→r) এবং (−→p−→q+→r) ভেক্টর তিনটির অভিমুখে →s ভেক্টরের ভেক্টর উপাংশ x,y এবং z হয়, তবে 2x+y+z-এর মান নির্ণয় করো।
05:56View SolutionIf →p,→q and →r are perpendicular to →q+→r,→r+→p and →p+→q respectively and if |→p+→q|=6,|→q+→r|=4√3 and |→r+→p|=4 then |→p+→q+→r| is
02:40View Solution→P,→Q,→R,→S are vector of equal magnitude. If →P+→Q−→R=0 angle between →P and →Q is θ1 . If →P+→Q−→S=0 angle between →P and →S is θ2 . The ratio of θ1 to θ2 is
03:37View SolutionSuppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is
02:04View Solution

