If the equation ∣∣x2+bx+c∣∣=k has four real roots, then b2−4c>0and0<k<4c−b24 b2−4c<0and0<k<4c−b24 b2−4c>0andk>4c−b24 none of theseSolution in Bengali
b2−4c>0and−<k<4c−b24
b2−4c<0and−<k<4c−b24
b2−4c>0and−k>4c−b24
none of these
The correct Answer is:1
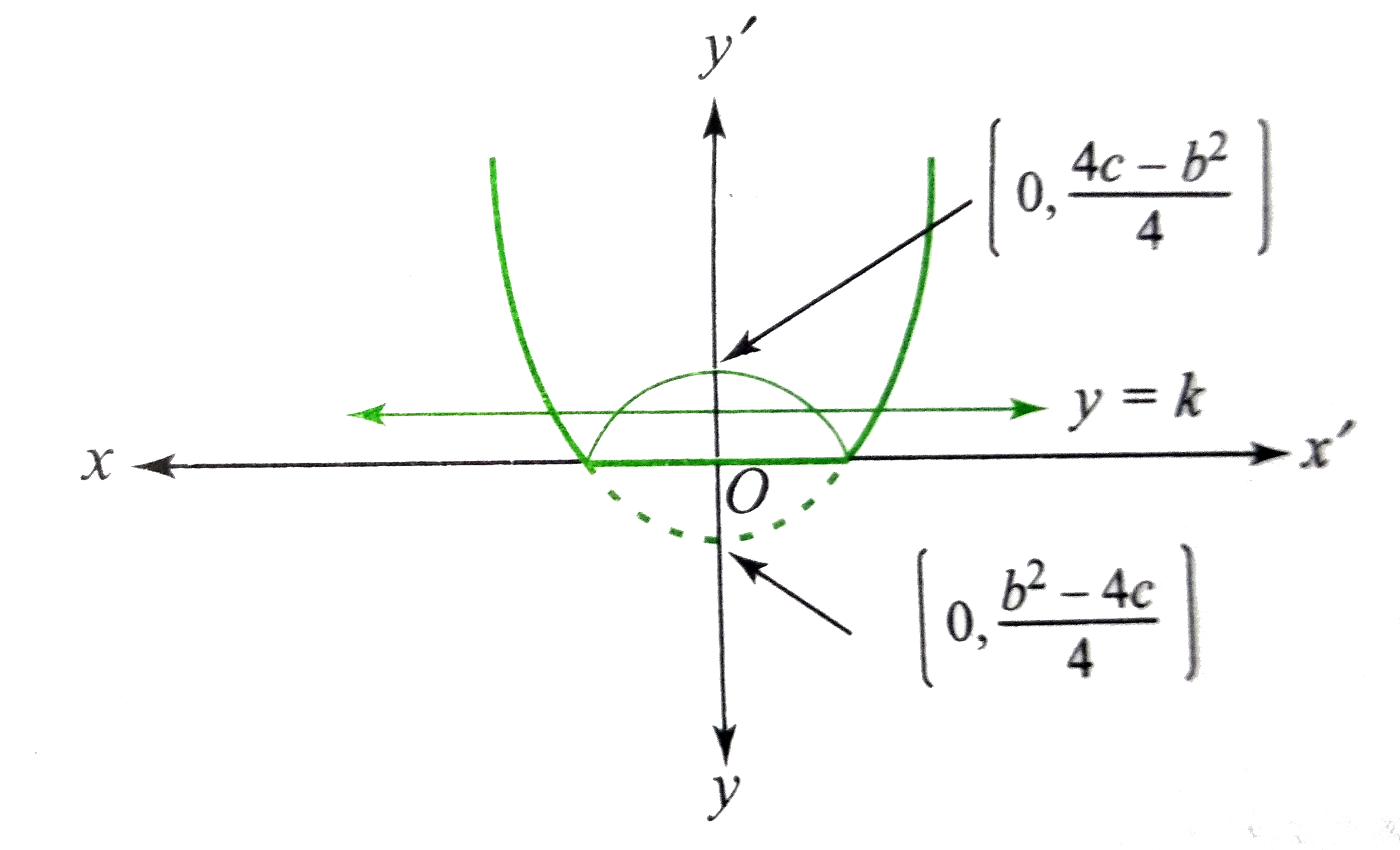
For the equation to have four real roots, the line y = k must
intersect y=∣∣x2=bx+c∣∣ at four point.
∴D>0andk∈(0,−D4)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type38videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Linked Comprechension Type37videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.139videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)1videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
If c≠0 and the equation p2x=ax+c+bx−c has two equal roots, then p can be
01:38View SolutionConsider an unknow polynomial which divided by (x−3) and (x−4) leaves remainder 2 and 1, respectively. Let R(x) be the remainder when this polynomial is divided by (x−3)(x−4).
If equations R(x)=x2+ax+1 has two distint real roots, then exhaustive values of a are.05:00View SolutionFind the values of a if x2−2(a−1)x+(2a+1)=0 has positive roots.
03:29View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
01:50View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
03:57View Solutiona^(2)+b^(2)+4c^(2)=2a+2b-4c+3=0
00:35View SolutionIf both roots of the equation ax2+x+c−a=0 are imaginary and c>−1, then a.3a>2+4c b.3a<2+4c c.c<a d. none of these
02:16View SolutionIf the equation ∣∣x2+bx+c∣∣=k has four real roots, then
A. b2−4c>0and0<k<4c−b24
B. b2−4c<0and0<k<4c−b24
C.b2−4c>0andk>4c−b24
D. none of these02:14View Solutiona^(2)-b^(2)-4bc+4c^(2)
04:44View SolutionConsider a circle x2+y2+ax+by+c=0 lying completely in the first quadrant. If m1andm2 are the maximum and minimum values of yx for all ordered pairs (x,y) on the circumference of the circle, then the value of (m1+m2) is (a)a2−4cb2−4c (b) 2abb2−4c (c)2ab4c−b2 (d) 2abb2−4ac
04:15View Solutionb^(2)+c^(2)+2bc+4b+4c
03:43View Solutiona2−b2−4ac+4c2
03:20View SolutionIf the roots of the equation x2−bx+c=0 are two consecutive integers, then find the value of b2−4c
08:54View SolutionIf the equation ∣∣x2+bx+c∣∣=k has four real roots, then
A. b2−4c>0and0<k<4c−b24
B. b2−4c<0and0<k<4c−b24
C.b2−4c>0andk>4c−b24
D. none of these02:06View SolutionConsider a circle x2+y2+ax+by+c=0 lying completely in the first quadrant. If m1andm2 are the maximum and minimum values of yx for all ordered pairs (x,y) on the circumference of the circle, then the value of (m1+m2) is (a)a2−4cb2−4c (b) 2abb2−4c (c)2ab4c−b2 (d) 2abb2−4ac
06:49View SolutionIf the equation ∣∣x2+bx+c∣∣=k has four real roots, then a. b2−4c>0 and 0<k<4c−b24 b. b2−4c<0 and 0<k<4c−b24 c. b2−4c>0 and k>4c−b24 d. none of these
04:02View Solution

