consider the graph of y=g(x)=f'(x) given that f(c ) =0, where y=f(x) is a polynomial funtion
The graph of y=f(x) will intersect the x axis
A
twice
B
once
C
never
D
none of these
Text Solution
The correct Answer is:2
f(X)≤0∀x∈[a,b] so f(X) is a decreasing funciton and f(c )=0 Thus f(x) cuts x axis once whne x=c
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type11videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Numerical Value Type24videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Multiple correct answers type48videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Multiple Correct Answer Type7videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The graph of y=f(x) is given below
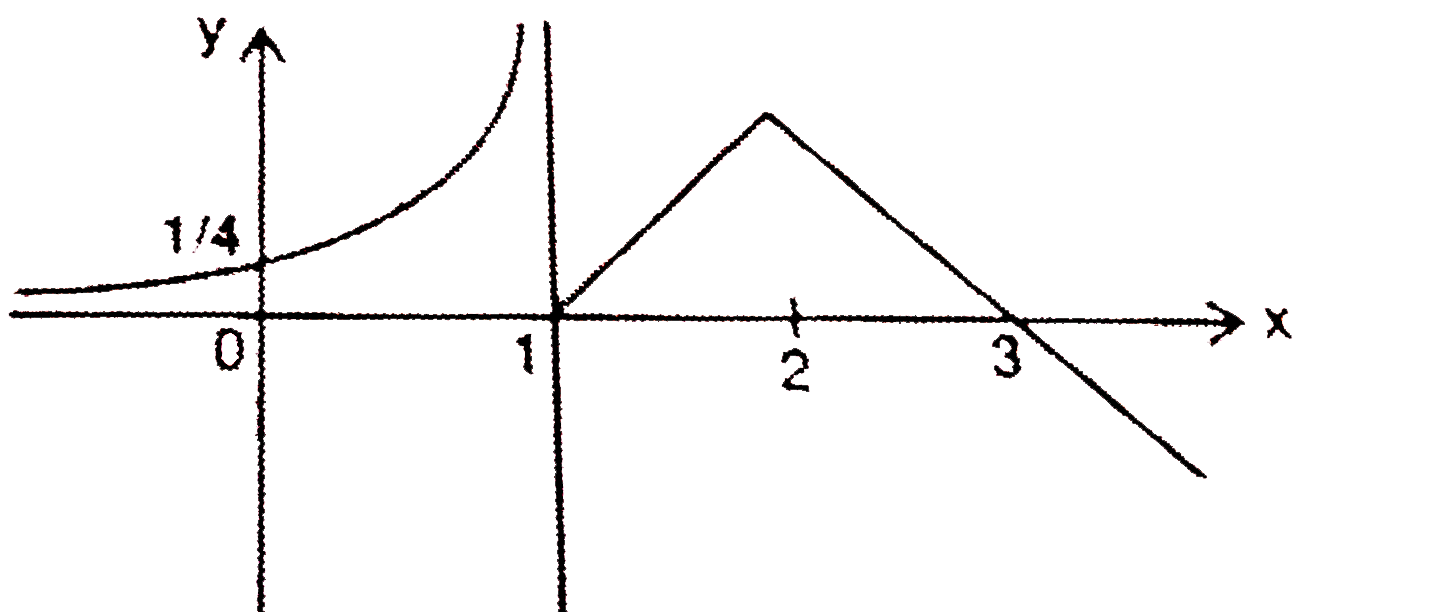
then the graph y=|f(|x|)| is :A
B
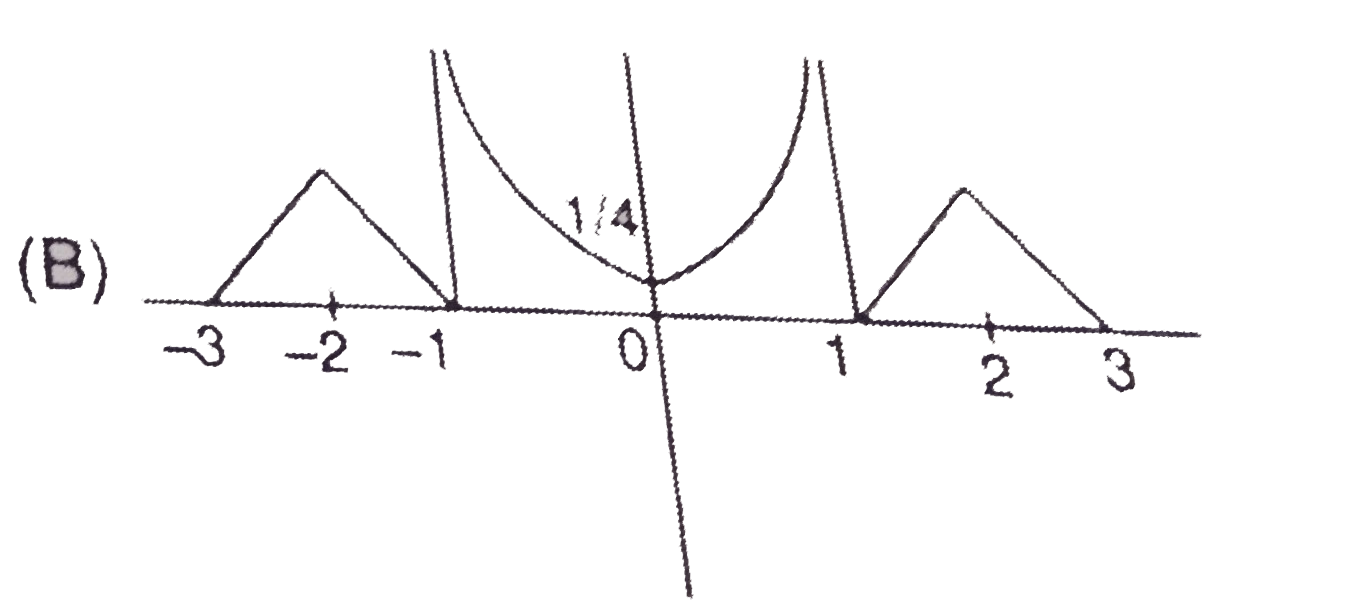C
Dnone of these - Question 2 - Select One
If f (x) is an even function, then the graph y = f (x) will be symmetrical about
Ax-axisBy-axisCBoth the axesDNone of these
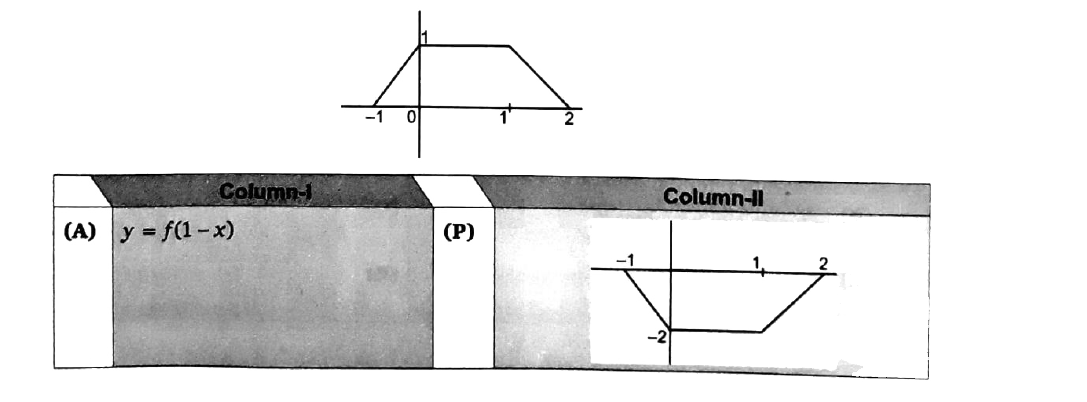
Graph of y=f(x) is given, then
View SolutionThe graph of y=f(x) is given below
then the graph y=|f(|x|)| is :View SolutionThe graph y = f (x) is as shown:
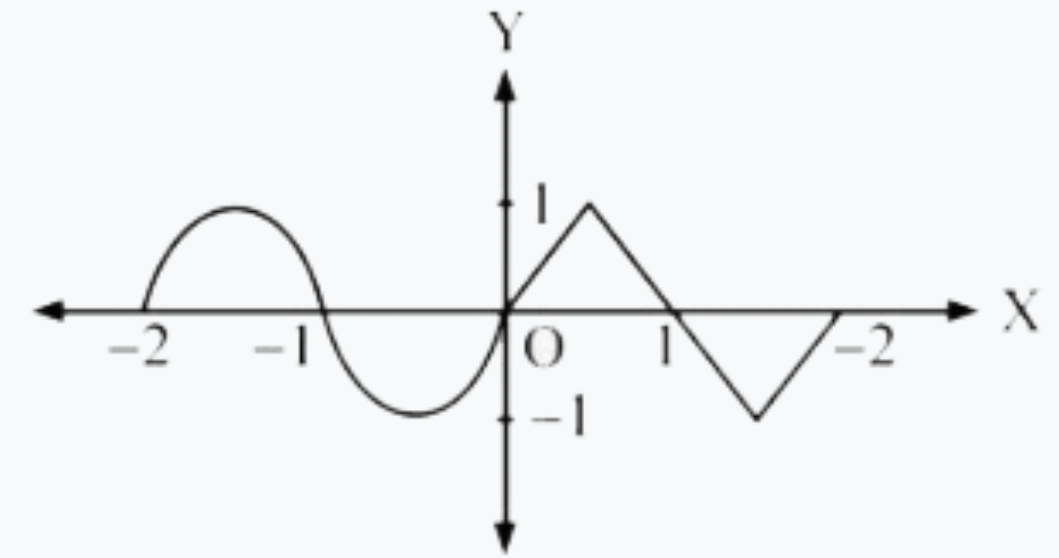
The graph of y = f (–|x|) is:View SolutionThe graph y = f (x) is as shown:
The graph of y = f (–|x|) is:View SolutionIf the graph of y=|f(x)| is as shown in figure
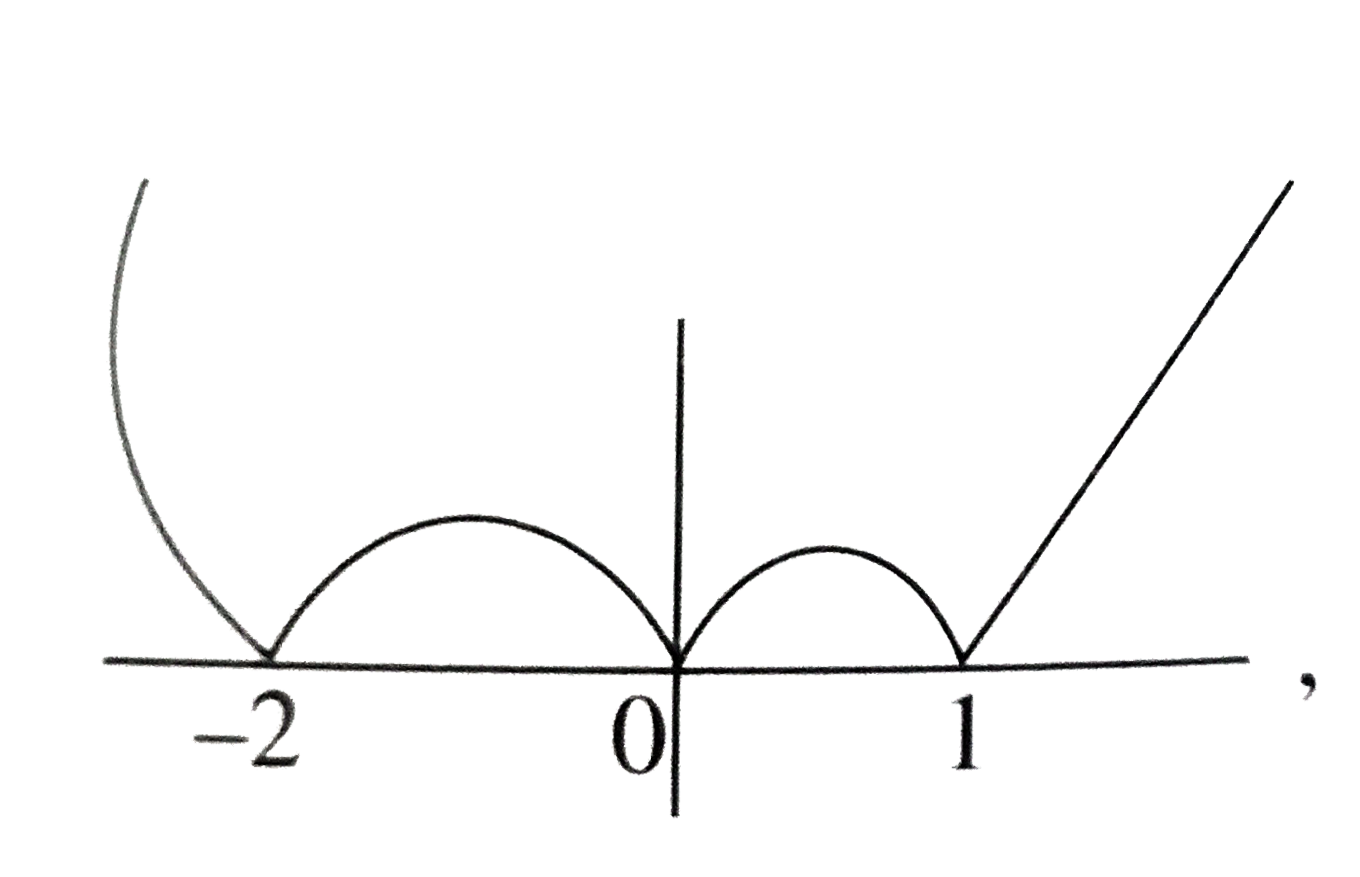then the graph of y=f(x) may be View SolutionIf the graph of y=|f(x)| is as shown in figure
then the graph of y=f(x) may be View Solution