A student got 85,87,91,82, 90 and x marks in all his subjects. His average marks were found to be 85. What should come in place of x ?
83
75
77
73
The correct Answer is:B
To find the value of x in the given problem, we will follow these steps:
Step 1: Understand the average formula
The average (A) of a set of numbers is calculated using the formula:
A=Total MarksNumber of Subjects
Step 2: Identify the given values
In this case, the average marks are given as 85, and the marks obtained by the student in five subjects are 85, 87, 91, 82, and 90. We also have the unknown marks x.
Step 3: Count the total number of subjects
The total number of subjects is 6 (5 known marks + 1 unknown mark x).
Step 4: Set up the equation using the average formula
Using the average formula, we can set up the equation:
85=85+87+91+82+90+x6
Step 5: Calculate the total marks without x
First, we calculate the sum of the known marks:
85+87+91+82+90=435
Step 6: Substitute the total marks into the equation
Now, substitute the total marks into the equation:
85=435+x6
Step 7: Multiply both sides by 6 to eliminate the fraction
To eliminate the fraction, multiply both sides by 6:
85×6=435+x
510=435+x
Step 8: Solve for x
Now, isolate x by subtracting 435 from both sides:
x=510−435
x=75
Conclusion
The value of x should be 75.
---
The average (A) of a set of numbers is calculated using the formula:
A=Total MarksNumber of Subjects
In this case, the average marks are given as 85, and the marks obtained by the student in five subjects are 85, 87, 91, 82, and 90. We also have the unknown marks x.
The total number of subjects is 6 (5 known marks + 1 unknown mark x).
Using the average formula, we can set up the equation:
85=85+87+91+82+90+x6
First, we calculate the sum of the known marks:
85+87+91+82+90=435
Now, substitute the total marks into the equation:
85=435+x6
To eliminate the fraction, multiply both sides by 6:
85×6=435+x
510=435+x
Now, isolate x by subtracting 435 from both sides:
x=510−435
x=75
The value of x should be 75.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGE EXERCISE - SELF ASSESSMENT SHEET -1610videos
AVERAGE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGE EXERCISE - UNIT TEST -320videos
AVERAGE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGE EXERCISE - UNIT TEST -320videos
AVERAGE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - ALGEBRIC IDENTITIESEXERCISE - Self Assessment Sheet-710videos
ALGEBRIC IDENTITIES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - UNIT TEST20videos
CIRCLES
Similar Questions
An examination was held on five subjects where the maximum marks for each subject was 100. X scored 82, 97, 88 and 91 marks in four subjects. If his total marks were 90% then, find his marks in the fifth subject.
पांच विषयों पर एक परीक्षा आयोजित की गई जहाँ प्रत्येक विषय के लिए अधिकतम अंक 100 थे | X ने 4 विषयों में क्रमश: 82, 97, 88 और 91 अंक प्राप्त किए | यदि उसके कुल अंक 90% थे, तो पांचवें विषय में उसने कितने अंक प्राप्त किए ?View SolutionA student obtain 75%,80%and85% in three subjects if the marks of another subject are added. Then the average cannot be less than
View Solution
Knowledge Check
- Question 1 - Select One
A student obtain 75%, 80% and 85% marks in three subjects. If the marks of another subject are added, then his average cannot be less than
A60%B65%C80%D90% - Question 2 - Select One
What is the average of marks obtained by all the students in subject B?
A71.4B73.14C107.14D114.07 - Question 3 - Select One
Question Stimulus
Ansy scored 87, 86, 92 and 95 marks in four subjects. What should be her least score in the fifth subject if she has to get a mean score of 90 in all?A95B89C93D90
The table given below represents the marks obtained by 5 students in 4 different subjects. Each student was given marks out of 100 in each of the given subjects.
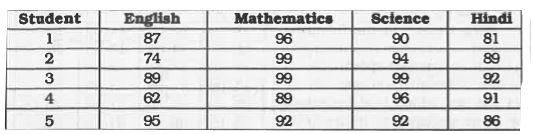
The average marks per student in English is what per cent of the average marks per student in Hindi ?View SolutionTotal of Arun’s marks in Sanskrit and Mathematics together are 80 more than his marks in Science. His average marks in the three subjects are 100. What are his marks in Science? (a) 80 (b) 110 (c) 120 (d) Data inadequate (e) None of these
View SolutionThe line chart given below shows the marks scored by 2 students P and Q in five subjects.
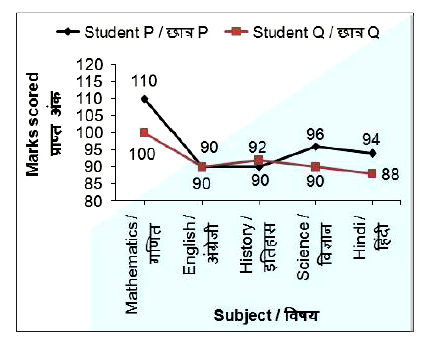
What is the average marks scored by student P in all the 5 subjects?View SolutionA student got 430 marks in five subjects. How many marks did he get in English ?
(I) His average marks in other four subjects is 84.
(II) His marks in English is 8 more than his average marks in five subject.View SolutionIn a class of 100 students, there are 70 boys whose average marks in a subject is 75. If the average marks of the complete class is 72, then what is the average of the girls ?
View Solution

