L M is a straight line and O is a point on LM .Line ON us drawn not coinciding with OL or OM .If ∠MON is three times ∠LON, then ∠MON is equal to :
45∘
60∘
105∘
135∘
The correct Answer is:D
To solve the problem step by step, we will define the angles and use the properties of straight lines and linear pairs.
1. Define the Angles:
Let ∠LON=x degrees. According to the problem, ∠MON is three times ∠LON. Therefore, we can express ∠MON as:
∠MON=3x degrees
2. Use the Linear Pair Property:
Since LM is a straight line, the angles ∠LON and ∠NOM (which is the same as ∠MON) form a linear pair. The sum of angles in a linear pair is 180 degrees. Thus, we can write:
∠LON+∠NOM=180 degrees
Substituting the angles we defined:
x+3x=180
3. Combine Like Terms:
Combining the terms gives:
4x=180
4. Solve for x:
To find x, divide both sides by 4:
x=1804=45 degrees
5. Find ∠MON:
Now that we have x, we can find ∠MON:
∠MON=3x=3×45=135 degrees
Final Answer:
Thus, ∠MON is equal to 135 degrees.
---
Let ∠LON=x degrees. According to the problem, ∠MON is three times ∠LON. Therefore, we can express ∠MON as:
∠MON=3x degrees
Since LM is a straight line, the angles ∠LON and ∠NOM (which is the same as ∠MON) form a linear pair. The sum of angles in a linear pair is 180 degrees. Thus, we can write:
∠LON+∠NOM=180 degrees
Substituting the angles we defined:
x+3x=180
Combining the terms gives:
4x=180
To find x, divide both sides by 4:
x=1804=45 degrees
Now that we have x, we can find ∠MON:
∠MON=3x=3×45=135 degrees
Thus, ∠MON is equal to 135 degrees.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINES AND ANGLES EXERCISE - SELF ASSESSMENT SHEET10videos
LINES AND ANGLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINES AND ANGLES EXERCISE - SELF ASSESSMENT SHEET10videos
LINES AND ANGLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - Unit Test -220videos
LINEAR EQUATIONS IN ONE VARIABLE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - NUMBERSEXERCISE - SELF ASSESSMENT SHEET-110videos
NUMBERS
Similar Questions
Two points A (a, 0) and B (0, b) are given, O is the origin and M is a point on the line joining AB such that ∠OMA is a right angle. If |OM|=8, then AM. BM is equal to
View SolutionLet ABC be a triangle in which AB = AC. Let L be the locus of points X inside or on the triangle such that BX = CX. Which of the following statements are correct?
1. L is a straight line passing through A and in-centre of triangle ABC is on L.
2. L is a straight line passing through A and orthocentre of triangle ABC is a point on L.
3. L is a straight line passing through A and centroid of triangle ABC is a point on L.
Select the correct answer using the code given below.View Solution
Knowledge Check
- Question 1 - Select One
AB is a straight line and O is a point on AB, if a line OC is drawn not coinciding with OA or OB, then ∠AOC and ∠BOC are
AequalBcomplementaryCsupplementaryDtogether equal to 100 - Question 2 - Select One
AB is a straight line and O is a point on AB, if a line OC is drawn not coinciding with OA or OB, then ∠AOC and ∠BOC are
AequalBcomplementaryCsupplementaryDtogether equal to 100 - Question 3 - Select One
O is point on the line LM A line ON is drawn which is neither coincident with OL nor with OM if ∠MON is one third of ∠LON then ∠MON equal to
AA)45∘BB)60∘CC)75∘DD)80∘
Straight lines are drawn by joining m points on a straight line of n points on another line. Then excluding the given points, the number of point of intersections of the lines drawn is (no tow lines drawn are parallel and no these lines are concurrent). a. 4mn(m−1)(n−1) b. 12mn(m−1)(n−1) c. 12m2n2 d. 14m2n2
View SolutionAB is a straight line and O is a point lying on AB .A line OC is drawn from O such that ∠COA=36∘. OD is a line within ∠COA such that ∠DOA=13
∠COA . If OE is a line within the ∠BOC,∠BOE=14∠BOC , then ∠DOE must beView SolutionIn the given figure, straight lines AB and CD intersect at O.If ∠β = 3∠p,then ∠p is equal to
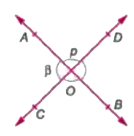 View Solution
View SolutionThere are m points on a straight line AB & n points on the line AC none of them being the point A. Tri- angles are formed with these points as vertices, when
A is excluded (ii) A is included.
The ratio of number of triangles in the two cases isView SolutionThree charge q,Q and −4q are placed in a straight line , line of length Lat points distant 0,L/2 and L respectively from one end. In order to make the net force on q zero, the charge Q must be equal to
View Solution

