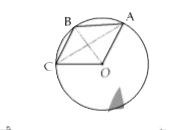
A rhombus OABC is drawn inside a circle whose centre is at O in such a way that the vertices A, B and C of the rhombus are on the circle. If the area of the rhombus is 32√3m2, then the radius of the circle is
64 m
8 m
3 m
46 m
The correct Answer is:B
To find the radius of the circle in which the rhombus OABC is inscribed, we can follow these steps:
1. Understanding the Problem:
We have a rhombus OABC inscribed in a circle with center O. The vertices A, B, and C are on the circle. We know the area of the rhombus is 32√3m2.
2. Identifying the Properties of the Rhombus:
In a rhombus, all sides are equal. Let the radius of the circle be r. Therefore, the lengths of the sides OA, OB, OC (which are also the sides of the rhombus) are equal to r.
3. Using the Area of the Rhombus:
The area A of a rhombus can also be expressed in terms of its diagonals d1 and d2:
A=12×d1×d2
However, we will also use the property of triangles formed by the diagonals.
4. Dividing the Rhombus into Triangles:
The diagonals of the rhombus divide it into four triangles of equal area. Thus, the area of the rhombus can be expressed as:
Area of Rhombus=2×Area of Triangle OAB
Given that the area of the rhombus is 32√3m2, we have:
2×Area of Triangle OAB=32√3
Therefore, the area of Triangle OAB is:
Area of Triangle OAB=16√3m2
5. Calculating the Area of Triangle OAB:
The area of triangle OAB can also be expressed using the formula:
Area=12×OA×OB×sin(∠AOB)
Since OA = OB = r, we can write:
Area of Triangle OAB=12×r×r×sin(∠AOB)=r22sin(∠AOB)
6. Setting Up the Equation:
From the area of Triangle OAB:
r22sin(∠AOB)=16√3
Thus, we can rearrange this to find:
r2sin(∠AOB)=32√3
7. Finding the Value of r:
Since the rhombus is symmetric and inscribed in a circle, the angle AOB can be calculated as 60∘ (as the rhombus divides the circle into equal angles). Therefore, sin(60∘)=√32:
r2⋅√32=32√3
Simplifying this gives:
r2=32√3⋅2√3=64
Thus, taking the square root:
r=√64=8m
Final Answer:
The radius of the circle is 8m.
We have a rhombus OABC inscribed in a circle with center O. The vertices A, B, and C are on the circle. We know the area of the rhombus is 32√3m2.
In a rhombus, all sides are equal. Let the radius of the circle be r. Therefore, the lengths of the sides OA, OB, OC (which are also the sides of the rhombus) are equal to r.
The area A of a rhombus can also be expressed in terms of its diagonals d1 and d2:
A=12×d1×d2
However, we will also use the property of triangles formed by the diagonals.
The diagonals of the rhombus divide it into four triangles of equal area. Thus, the area of the rhombus can be expressed as:
Area of Rhombus=2×Area of Triangle OAB
Given that the area of the rhombus is 32√3m2, we have:
2×Area of Triangle OAB=32√3
Therefore, the area of Triangle OAB is:
Area of Triangle OAB=16√3m2
The area of triangle OAB can also be expressed using the formula:
Area=12×OA×OB×sin(∠AOB)
Since OA = OB = r, we can write:
Area of Triangle OAB=12×r×r×sin(∠AOB)=r22sin(∠AOB)
From the area of Triangle OAB:
r22sin(∠AOB)=16√3
Thus, we can rearrange this to find:
r2sin(∠AOB)=32√3
Since the rhombus is symmetric and inscribed in a circle, the angle AOB can be calculated as 60∘ (as the rhombus divides the circle into equal angles). Therefore, sin(60∘)=√32:
r2⋅√32=32√3
Simplifying this gives:
r2=32√3⋅2√3=64
Thus, taking the square root:
r=√64=8m
The radius of the circle is 8m.
Topper's Solved these Questions
- AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS EXERCISE - Self Assessment Sheet-25 (Chapters 25 and 26)
10 Videos
- AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS EXERCISE - Self Assessment Sheet-25 (Chapters 25 and 26)
10 Videos
- AREA AND PERIMETER OF RECTANGLE, SQUARE, PARALLELOGRAM, TRIANGLE AND CIRCLESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AREA AND PERIMETER OF RECTANGLE, SQUARE, PARALLELOGRAM, TRIANGLE AND CIRCLESEXERCISE - Question Bank - 25 (M.C.Q)
15 Videos
- AVERAGEBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGEEXERCISE - SELF ASSESSMENT SHEET
10 Videos
Similar Questions
Knowledge Check
OABC is a rhombus whose the vertices A, B and C lie on a circle of radius 10cm and with centre O. Find the area of the rhombus.
A30√3cm2B50√3cm2C10√3cm2D100√3cm2
A rhombus has the same perimeter as the circumference of a circle. If the side of the rhombus is 2.2 m. find the radius of the circle.
View SolutionA rhombus has the same perimeter as the circumference of a circle. If each side of the rhombus measures 33 cm, find the radius of the circle.
View SolutionABC is an equilateral triangle of side 6 cm, a circle, centre O, passes through the vertices A, B, and C. Find the radius of the circle.
View SolutionAll the vertices of a rhombus lie on a circle. Find the area of the rhombus, if area of the circle is 1256cm2 . (use π=3.14)
View SolutionIn a given figure, OABC is a rhombus which has 3 angles on circumference of circlewith centre O. If area of rhombus is 32√3cm2 then find radius of circle?
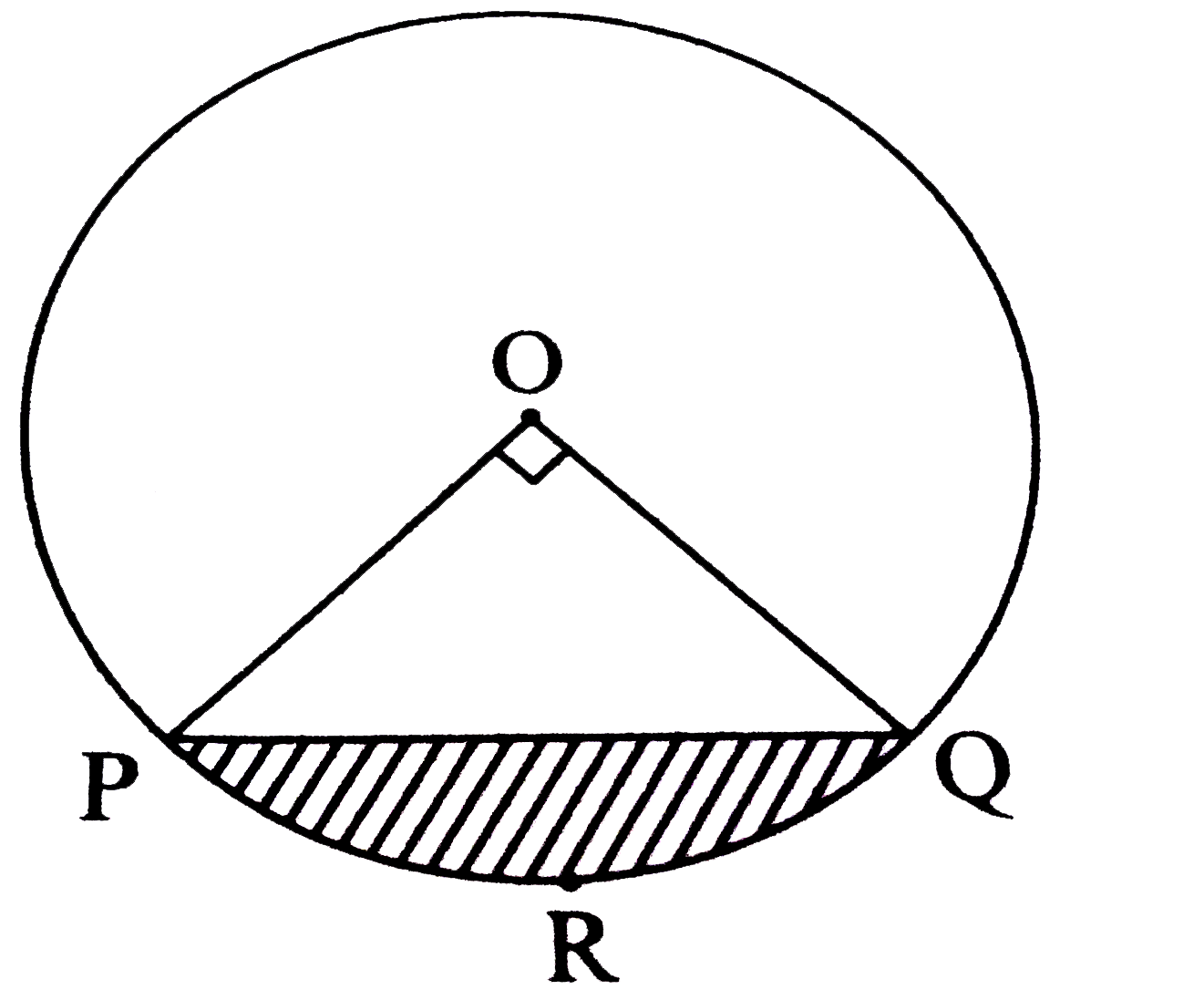
View SolutionIn the figure, O is the centre of the circle. ∠POQ=90∘ .
The area of the shaded region is 126cm2. Find the radius of the circle.
View SolutionOABC is a rhombus whose three vertices A,B and C lie on a cricle with centre O. If the radius of the circle is 10 cm. Find the ara of the rhombus
View Solution

