A slab of ice 8 inches in length, 11 inches in breadth and 2 inches thick was melted and resolidified in the form of a rod of 8 inches diameter. What is the length of such a rod in inches ?
The correct Answer is:3.5 inches.
To find the length of the rod formed from the melted slab of ice, we need to follow these steps:
Step 1: Calculate the volume of the slab of ice.
The volume V of a rectangular prism (the slab of ice) is given by the formula:
V=length×breadth×height
Here, the dimensions of the slab of ice are:
- Length = 8 inches
- Breadth = 11 inches
- Height (thickness) = 2 inches
Substituting the values:
V=8×11×2
V=176 cubic inches
Step 2: Calculate the volume of the rod.
The volume V of a cylinder (the rod) is given by the formula:
V=πr2h
where r is the radius and h is the height (length) of the cylinder.
The diameter of the rod is given as 8 inches, so the radius r is:
r=diameter2=82=4 inches
Now, we can express the volume of the rod in terms of its height h:
V=π(4)2h=16πh
Step 3: Set the volumes equal to each other.
Since the volume of the melted ice slab is equal to the volume of the rod:
176=16πh
Step 4: Solve for h.
To find h, we rearrange the equation:
h=17616π
Calculating h:
h=17616×3.14(using π≈3.14)
h=17650.24≈3.5 inches
Final Answer:
The length of the rod is approximately 3.5 inches.
---
The volume V of a rectangular prism (the slab of ice) is given by the formula:
V=length×breadth×height
Here, the dimensions of the slab of ice are:
- Length = 8 inches
- Breadth = 11 inches
- Height (thickness) = 2 inches
V=8×11×2
V=176 cubic inches
The volume V of a cylinder (the rod) is given by the formula:
V=πr2h
where r is the radius and h is the height (length) of the cylinder.
r=diameter2=82=4 inches
V=π(4)2h=16πh
Since the volume of the melted ice slab is equal to the volume of the rod:
176=16πh
To find h, we rearrange the equation:
h=17616π
h=17616×3.14(using π≈3.14)
h=17650.24≈3.5 inches
The length of the rod is approximately 3.5 inches.
Topper's Solved these Questions
- VOLUME AND SURFACE AREA BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - VOLUME AND SURFACE AREA EXERCISE - Section A (Question Bank - 27)
20 Videos
- VOLUME AND SURFACE AREA BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - VOLUME AND SURFACE AREA EXERCISE - Section B (Question Bank - 27)
28 Videos
- TRIGONOMETRICAL RATIOS OF STANDARD ANGLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLES EXERCISE - Self Assessment Sheet - 32
10 Videos
Similar Questions
Knowledge Check
The length of a string is 8 feet and 9 inches, which is divided into 3 equal parts. What is the length of each part in inches?
A31B33C35D37A cube which is painted red on the outer surface is of 2 inches height, 2 inches wide and 2 inches across. If it is cut into one-inch cubes as shown by dotted lines, indicate the number of cubes which are red on two sides only ?
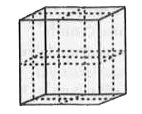 A4B6C8D0
A4B6C8D0A rectangular box is to be made form a sheet of 24 inch length and 9 inch wideth cutting out indetical squares of side length x from the four corners and turning up the sides
What is the value of x for width the vulume is maximum ?A1 inchB1.5 inchC2 inchD2.5 inch
A board of 7 ft. 9 inches long is divided into 3 equal parts. What is the length of each part?
View SolutionA cube which is painted red on the outer surface is of 2 inches height, 2 inches wide and 2 inches across. If it is cut into one-inch cubes as shown by dotted lines. indicate the number of cubes which are red on two sides only?
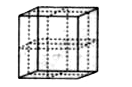 (A)4
(B)6
(C)8
(D)0
(A)4
(B)6
(C)8
(D)0
View SolutionA piece of metal is 3 inch (represented by in) long. What is its length in cm?
View SolutionA rectangular red carpet of size 6 ft. × 12 ft has a dark red border 6 inches wide. What is the area of the dark red border ?
View SolutionRead die following information carefully and answer the questions given below, A rectangular box is to be made from a sheet of 24 inch length and 9 inch width cutting out identical squares of side length x from ihe four corners and turning up the sides.
What is the value of x for which the volume is maximum?
View Solution
