The centre of the circle is at the origin and its radius is 10. Which of the following points lies inside the circle?
(6,8)
(0, 11)
(-10,0)
(7,7)
The correct Answer is:D
To determine which of the given points lies inside the circle with its center at the origin (0, 0) and a radius of 10, we can follow these steps:
Step 1: Understand the Circle's Equation
The equation of a circle with center at the origin (0, 0) and radius r is given by:
x2+y2=r2
In this case, since the radius r=10, the equation becomes:
x2+y2=100
Step 2: Identify the Points to Check
We need to check the following points to see if they lie inside the circle:
1. (6, 8)
2. (0, 11)
3. (-10, 0)
4. (7, 7)
Step 3: Calculate the Distance for Each Point
To determine if a point lies inside the circle, we calculate the distance from the origin using the distance formula:
d=√x2+y2
If d<10, the point lies inside the circle. If d=10, it lies on the circle, and if d>10, it lies outside the circle.
Check Point (6, 8):
d=√62+82=√36+64=√100=10
Since d=10, point (6, 8) lies on the circle.
Check Point (0, 11):
d=√02+112=√0+121=√121=11
Since d>10, point (0, 11) lies outside the circle.
Check Point (-10, 0):
d=√(−10)2+02=√100+0=√100=10
Since d=10, point (-10, 0) lies on the circle.
Check Point (7, 7):
d=√72+72=√49+49=√98≈9.9
Since d<10, point (7, 7) lies inside the circle.
Conclusion
The point that lies inside the circle is (7, 7).
The equation of a circle with center at the origin (0, 0) and radius r is given by:
x2+y2=r2
In this case, since the radius r=10, the equation becomes:
x2+y2=100
We need to check the following points to see if they lie inside the circle:
1. (6, 8)
2. (0, 11)
3. (-10, 0)
4. (7, 7)
To determine if a point lies inside the circle, we calculate the distance from the origin using the distance formula:
d=√x2+y2
If d<10, the point lies inside the circle. If d=10, it lies on the circle, and if d>10, it lies outside the circle.
d=√62+82=√36+64=√100=10
Since d=10, point (6, 8) lies on the circle.
d=√02+112=√0+121=√121=11
Since d>10, point (0, 11) lies outside the circle.
d=√(−10)2+02=√100+0=√100=10
Since d=10, point (-10, 0) lies on the circle.
d=√72+72=√49+49=√98≈9.9
Since d<10, point (7, 7) lies inside the circle.
The point that lies inside the circle is (7, 7).
Topper's Solved these Questions
- CO-ORDINATE GEOMETRYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Question Bank
20 Videos
- CIRCLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - UNIT TEST - 4
25 Videos
- COMPOUND INTEREST BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - COMPOUND INTEREST EXERCISE - Self Assessment Sheet - 19
10 Videos
Similar Questions
Fill in the blanks: All point lying inside/outside a circle are called ... points/ ... points. Circle having the same centre and different radii are called ... circles. A point whose distance from the centre of a circle is greater than its radius lies in .... of the circle. A continuous piece of a circle is .... of the circle. The longest chord of a circle is a ......of the circle. An arc is a ......... when its ends are the ends of a diameter. Segment of a circle is the region between an arc and ... of the circle. A circle divides the plane, on which it lies, in .... parts.
View SolutionA circle has its centre at the origin and a point P (5,0) lies on it . The point Q (6,8) lies outside the circle.
View Solution
Knowledge Check
What is the equation of a circle with centre of origin and radius is 6 cm?
Ax2+y2−y=36Bx2+y2−x−y=36Cx2+y2−36=0Dx2+y2−x=36The area of a circle is increased by 22 cm' when its radius is increased by 1 cm. The original radius of the circle is
A6cmB3.2cmC3cmD3.5cmWhich one of the following points lies inside a circle of radius 6 and centre at (3,5) ?
A(−2,−1)B(0,1)C(−1,−2)D(2,−1)
In given figure, O is the centre of the circle.
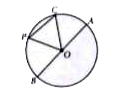
Which of the following is not the radius of the given circle?
View SolutionFill in the blanks:(i) The centre of a circle lies in of the circle. (exterior/ interior)(ii) A point, whose distance from the centre of a circle is greater than its radius lies inof the circle. (exterior/ interior)(iii) The longest chord of a circle is a_________ of the circle.(iv) An arc is a _________when its ends are the ends of a diameter.(v) Segment of a circle is the region between an arc and________ of the circle.(vi) A circle divides the plane, on which it lies, in________ parts.
View SolutionFill in the blanks: (i) The centre of a circle lies in of the circle. (exterior/ interior) (ii) A point, whose distance from the centre of a circle is greater than its radius lies in of the circle. (exterior/ interior) (iii) The longest cho
View SolutionA square is inscribed in a circle. If pr is the probability that a randomly chosen point inside the circle lies within the square and p, is the probability that the point lies outside the square, then
View SolutionThe line y=√3x+4 touches a circle with centre at the origin. Find the radius of the circle.
View Solution
