Magnetic poles always exist as
dipole
monopole
no-pole
none of these
Step-by-Step Solution:
1. Understanding Magnetic Poles:
- Every magnet has two distinct regions known as poles: the North Pole and the South Pole. These poles are where the magnetic force is strongest.
2. Definition of a Magnetic Dipole:
- A magnetic dipole consists of two equal and opposite magnetic poles separated by a distance. This is the fundamental nature of all magnets.
3. Monopoles and Nopoles:
- A magnetic monopole would be a magnet with only one pole (either North or South), which does not exist in nature. Similarly, the term "nopole" suggests the absence of poles, which contradicts the basic definition of a magnet.
4. Conclusion:
- Since all magnets have two poles, they are classified as dipoles. Therefore, the statement "Magnetic poles always exist as" can only be answered as "Dipole".
5. Final Answer:
- The correct answer is Dipole.
---
- Every magnet has two distinct regions known as poles: the North Pole and the South Pole. These poles are where the magnetic force is strongest.
- A magnetic dipole consists of two equal and opposite magnetic poles separated by a distance. This is the fundamental nature of all magnets.
- A magnetic monopole would be a magnet with only one pole (either North or South), which does not exist in nature. Similarly, the term "nopole" suggests the absence of poles, which contradicts the basic definition of a magnet.
- Since all magnets have two poles, they are classified as dipoles. Therefore, the statement "Magnetic poles always exist as" can only be answered as "Dipole".
- The correct answer is Dipole.
Topper's Solved these Questions
- MAGNETISMBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - MAGNETISMEXERCISE - SELF ASSESSMENT SHEET-6
31 Videos
- LIGHTBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - SELF ASSESSMENT SHEET -4
24 Videos
- MEASUREMENT AND MOTIONBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - MEASUREMENT AND MOTIONEXERCISE - Self Assessment Sheet -1 (a)
14 Videos
Similar Questions
Statement-A: The points of the magnet where there is maximum attraction are called the poles of the magnet
Statement-B : Magnetic poles always exist in pairs
View SolutionA physics teacher explains Gauss's theorem in electrostatics and Gauss's theorem in magnetism to his students in a class. He tells them that total normal electric flux over a closed surface in vacuum is ϕe=Q∈0, where Q is algebraic sum of charges inside the surface. Further, total normal magnetic flux over a closed surface in vacuum is always zero. The teacher emphasises that this is because in magnetism, poles always exist in unlike pairs of equal strengh, i.e., isolated magnetic poles called monopoles do not exist.
Read the above passage and answer the following questions:
(i) What are the implications of Gauss's theorem in magnetism in day to day life?
(ii) Two magnetic dipoles of moments 5Am2 and 3Am2 oriented along opposite directions are enclosed in a surface. What is total normal magnetic flux over this surface?
(iii) Two point charges +4q and −q are enclosed in a surface in vacuum, and third charge 5q lies outside the surface. What is total normal electric flux over the surface?
View Solution
Knowledge Check
Assertion : If a magnet is rolled in a packet of steel pins, the pins will get most attracted to the poles of a magnet.
Reason : Poles always exist in pairs.AIf both assertion and reason are true and reason is the correct explanation of assertion .BIf both assertion and reason are true but reason is not the correct explation of assertion.CIf assertion is true but reason is falseDIf assertion is false but reason is true.
Magnetic poles exist in pairs.
View SolutionMagnetic poles exist in pairs. State true / false. Explain using the example of a bar magnet.
View SolutionWhy do magnetic field lines always exist in close loops?
View SolutionMagnetic poles exist in pair. We cannot get a magnetic monopole. When we cut a magnet, each piece will behave like a magnet with two poles
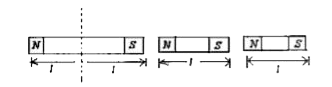
Based on the above, answer the following Questions
A bar magnet is cut as shown in the figure. Mark the polarity of each pole (from left to right) for the polarity missed piece
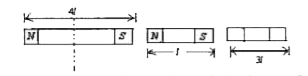
View SolutionMagnetic poles exist in pair. We cannot get a magnetic monopole. When we cut a magnet, each piece will behave like a magnet with two poles

Based on the above, answer the following Questions
A bar magnet is cut as shown in the figure. Mark the polarity of each pole (from left to right) for polarity missed piece
View SolutionCan magnetic poles exist in isolation?
View SolutionDo two distinct poles actually exist at two nearby points in a magnetic dipole?
View Solution
