Surbhi sets up the apparatus as shown to test the electrical conductivity of vinegar. She finds that the current passing through the circuit is not strong enough to make the bulb glow. What other device could she use in place of the bulb so that it glows even under weak current
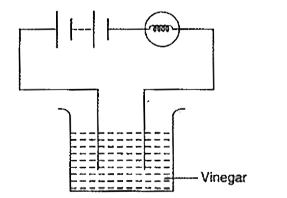
The bulb, may be féplacèd by LED which glows even under weak current in the circuit.
Similar Questions
Read the following text and answer the following questions on the basis of the same:
Shunt resistance: The ammeter shunt is the device which provides the low resistance path to the flow of current. It is connected in parallel with the ammeter. In some ammeter the shunt is in-built inside the instrument while in others it is externally connected to the circuit.
Ammeters are designed for measurement of low current. For measuring high current, the shunt is connected in parallel to the ammeter. The significant portion of the current passes to the shunt because of the low resistance path and little amount of current passes through the ammeter.
The shunt is connected in parallel to the ammeter because of which the voltage drops across the meter and shunt remain the same. Thus, the movement of the pointer is not affected by the shunt.
Let us consider that the current to be measured is I. The circuit has ammeter and shunt connected parallel to each other. The ammeter is designed for measurement of small current say, Im. The magnitude of the current I passes through the meter is very high, and it will burn the meter. So, for measuring the current I the shunt is required in the circuit.
As the shunt connects in parallel with the ammeter, thus the same voltage drops occur between them:
IShRSH=ImRm
∴RSH=ImRm/ISH
Shunt current ISH=I−Im
So, RSH=ImRm/(I−Im)
∴I/Im=1+(Rm/RSH)
The ratio of the total current to the current required for the movement of the ammeter coil is called the multiplying power of the shunt.
∴ The multiplying power =m=I/Lm
RSH=Rm/(m−1)
The following are the requirements of the shunt.
• The resistance of the shunt should remain constant with time.
• The temperature of the material-should remain same even though substantial current flows through the circuit.
What will be the value of the shunt resistance if the ammeter coil resistance is 1Ω and multiplying power is 100?View SolutionRead the following text and answer the following questions on the basis of the same:
Shunt resistance: The ammeter shunt is the device which provides the low resistance path to the flow of current. It is connected in parallel with the ammeter. In some ammeter the shunt is in-built inside the instrument while in others it is externally connected to the circuit.
Ammeters are designed for measurement of low current. For measuring high current, the shunt is connected in parallel to the ammeter. The significant portion of the current passes to the shunt because of the low resistance path and little amount of current passes through the ammeter.
The shunt is connected in parallel to the ammeter because of which the voltage drops across the meter and shunt remain the same. Thus, the movement of the pointer is not affected by the shunt.
Let us consider that the current to be measured is I. The circuit has ammeter and shunt connected parallel to each other. The ammeter is designed for measurement of small current say, Im. The magnitude of the current I passes through the meter is very high, and it will burn the meter. So, for measuring the current I the shunt is required in the circuit.
As the shunt connects in parallel with the ammeter, thus the same voltage drops occur between them:
IShRSH=ImRm
∴RSH=ImRm/ISH
Shunt current ISH=I−Im
So, RSH=ImRm/(I−Im)
∴I/Im=1+(Rm/RSH)
The ratio of the total current to the current required for the movement of the ammeter coil is called the multiplying power of the shunt.
∴ The multiplying power =m=I/Lm
RSH=Rm/(m−1)
The following are the requirements of the shunt.
• The resistance of the shunt should remain constant with time.
• The temperature of the material-should remain same even though substantial current flows through the circuit.
How shunt is connected with a ammeter?View Solution
Knowledge Check
- Question 1 - Select One
What is the thin wire In the bulb which glows when an electric current passes through It called?
AFilamentBHolderCConnecting wireDElement - Question 2 - Select One
Read the following text and answer the following questions on the basis of the same:
Shunt resistance: The ammeter shunt is the device which provides the low resistance path to the flow of current. It is connected in parallel with the ammeter. In some ammeter the shunt is in-built inside the instrument while in others it is externally connected to the circuit.
Ammeters are designed for measurement of low current. For measuring high current, the shunt is connected in parallel to the ammeter. The significant portion of the current passes to the shunt because of the low resistance path and little amount of current passes through the ammeter.
The shunt is connected in parallel to the ammeter because of which the voltage drops across the meter and shunt remain the same. Thus, the movement of the pointer is not affected by the shunt.
Let us consider that the current to be measured is I. The circuit has ammeter and shunt connected parallel to each other. The ammeter is designed for measurement of small current say, Im. The magnitude of the current I passes through the meter is very high, and it will burn the meter. So, for measuring the current I the shunt is required in the circuit.
As the shunt connects in parallel with the ammeter, thus the same voltage drops occur between them:
IShRSH=ImRm
∴RSH=ImRm/ISH
Shunt current ISH=I−Im
So, RSH=ImRm/(I−Im)
∴I/Im=1+(Rm/RSH)
The ratio of the total current to the current required for the movement of the ammeter coil is called the multiplying power of the shunt.
∴ The multiplying power =m=I/Lm
RSH=Rm/(m−1)
The following are the requirements of the shunt.
• The resistance of the shunt should remain constant with time.
• The temperature of the material-should remain same even though substantial current flows through the circuit.
Manganin and Constantan are used for inaking the shunt of DC and AC ammeter respectively. What is multiplying power of the shunt?ATotal currentCurrent required by the movement of ammeter coilBCurrent required by the movement of ammeter coilTotal currentCCurrent required by the movement of ammeter coil X Total currentDNone of the above - Question 3 - Select One
Read the following text and answer the following questions on the basis of the same:
Shunt resistance: The ammeter shunt is the device which provides the low resistance path to the flow of current. It is connected in parallel with the ammeter. In some ammeter the shunt is in-built inside the instrument while in others it is externally connected to the circuit.
Ammeters are designed for measurement of low current. For measuring high current, the shunt is connected in parallel to the ammeter. The significant portion of the current passes to the shunt because of the low resistance path and little amount of current passes through the ammeter.
The shunt is connected in parallel to the ammeter because of which the voltage drops across the meter and shunt remain the same. Thus, the movement of the pointer is not affected by the shunt.
Let us consider that the current to be measured is I. The circuit has ammeter and shunt connected parallel to each other. The ammeter is designed for measurement of small current say, Im. The magnitude of the current I passes through the meter is very high, and it will burn the meter. So, for measuring the current I the shunt is required in the circuit.
As the shunt connects in parallel with the ammeter, thus the same voltage drops occur between them:
IShRSH=ImRm
∴RSH=ImRm/ISH
Shunt current ISH=I−Im
So, RSH=ImRm/(I−Im)
∴I/Im=1+(Rm/RSH)
The ratio of the total current to the current required for the movement of the ammeter coil is called the multiplying power of the shunt.
∴ The multiplying power =m=I/Lm
RSH=Rm/(m−1)
The following are the requirements of the shunt.
• The resistance of the shunt should remain constant with time.
• The temperature of the material-should remain same even though substantial current flows through the circuit.
Current through shunt isAgreater than current through ammeter coil.Bless than current through ammeter coil.Cequal to the current through ammeter coil.Dmay be greater than or equal to or less than current through ammeter coil.
Attempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
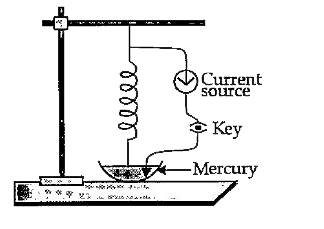
Roget's spiral:
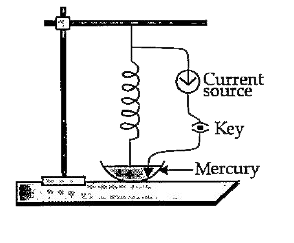
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What else can be used instead of mercury in Roget's spiral?
 View Solution
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
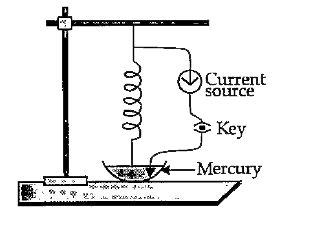
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What are main 3 components in a Roget's spiral?
 View Solution
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
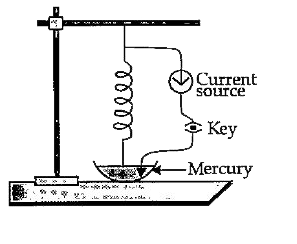
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Why the spring shrinks in Roget's spiral?
 View Solution
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Magnetic effects:
 View Solution
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
The force 10−3 N, is equivalent to:
 View Solution
View Solution

