Find the LCM of 40, 144 and 180.
To find the LCM (Least Common Multiple) of the numbers 40, 144, and 180 using the long division method, follow these steps:
Step 1: Prime Factorization
First, we need to find the prime factorization of each number.
- 40:
- 40 = 2 × 20
- 20 = 2 × 10
- 10 = 2 × 5
- So, the prime factorization of 40 is 23×51.
- 144:
- 144 = 12 × 12
- 12 = 3 × 4
- 4 = 2 × 2
- So, the prime factorization of 144 is 24×32.
- 180:
- 180 = 18 × 10
- 18 = 2 × 9
- 9 = 3 × 3
- 10 = 2 × 5
- So, the prime factorization of 180 is 22×32×51.
Step 2: Identify the Highest Powers
Next, we identify the highest power of each prime factor present in all the factorizations.
- For 2: The highest power is 24 (from 144).
- For 3: The highest power is 32 (from both 144 and 180).
- For 5: The highest power is 51 (from both 40 and 180).
Step 3: Calculate the LCM
Now, we multiply these highest powers together to find the LCM.
LCM=24×32×51
Calculating this step by step:
1. 24=16
2. 32=9
3. 51=5
Now multiply these results:
1. 16×9=144
2. 144×5=720
Final Answer
Thus, the LCM of 40, 144, and 180 is 720.
---
First, we need to find the prime factorization of each number.
- 40 = 2 × 20
- 20 = 2 × 10
- 10 = 2 × 5
- So, the prime factorization of 40 is 23×51.
- 144 = 12 × 12
- 12 = 3 × 4
- 4 = 2 × 2
- So, the prime factorization of 144 is 24×32.
- 180 = 18 × 10
- 18 = 2 × 9
- 9 = 3 × 3
- 10 = 2 × 5
- So, the prime factorization of 180 is 22×32×51.
Next, we identify the highest power of each prime factor present in all the factorizations.
- For 3: The highest power is 32 (from both 144 and 180).
- For 5: The highest power is 51 (from both 40 and 180).
Now, we multiply these highest powers together to find the LCM.
2. 32=9
3. 51=5
2. 144×5=720
Thus, the LCM of 40, 144, and 180 is 720.
Topper's Solved these Questions
- PLAYING WITH NUMBERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE (SUBJECTIVE PROBLEMS (SHORT ANSWER TYPE))
10 Videos
- PLAYING WITH NUMBERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE (SUBJECTIVE PROBLEMS (LONG ANSWER TYPE))
4 Videos
- PLAYING WITH NUMBERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE (COMPREHENSION TYPE (PASAGE-II))
3 Videos
- MENSURATIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Olympiad/HOTS Corner
20 Videos
- PRACTICAL GEOMETRY BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - EXERCISE (SUBJECTIVE PROBLEMS) (LONG ANSWER TYPE )
5 Videos
Similar Questions
Knowledge Check
Find the LCM of 96, 144 and 150.
A1140B3600C7200D2400
Find the LCM of 144 and 156.
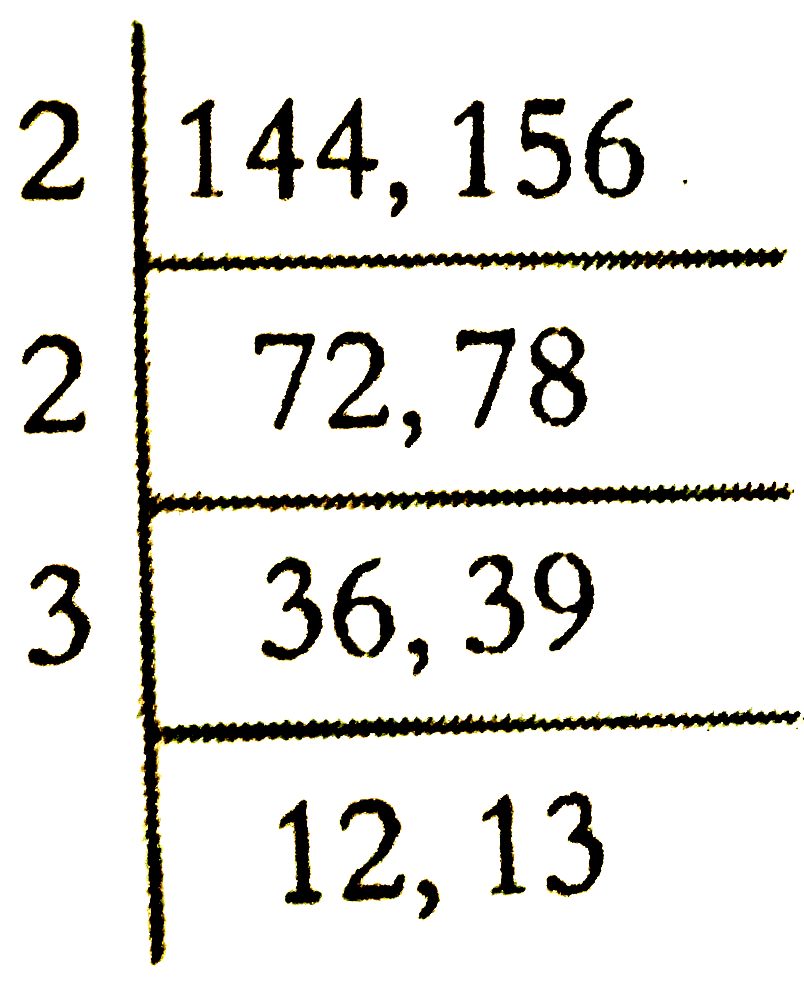
View SolutionFind the LCM of 144 and 156.
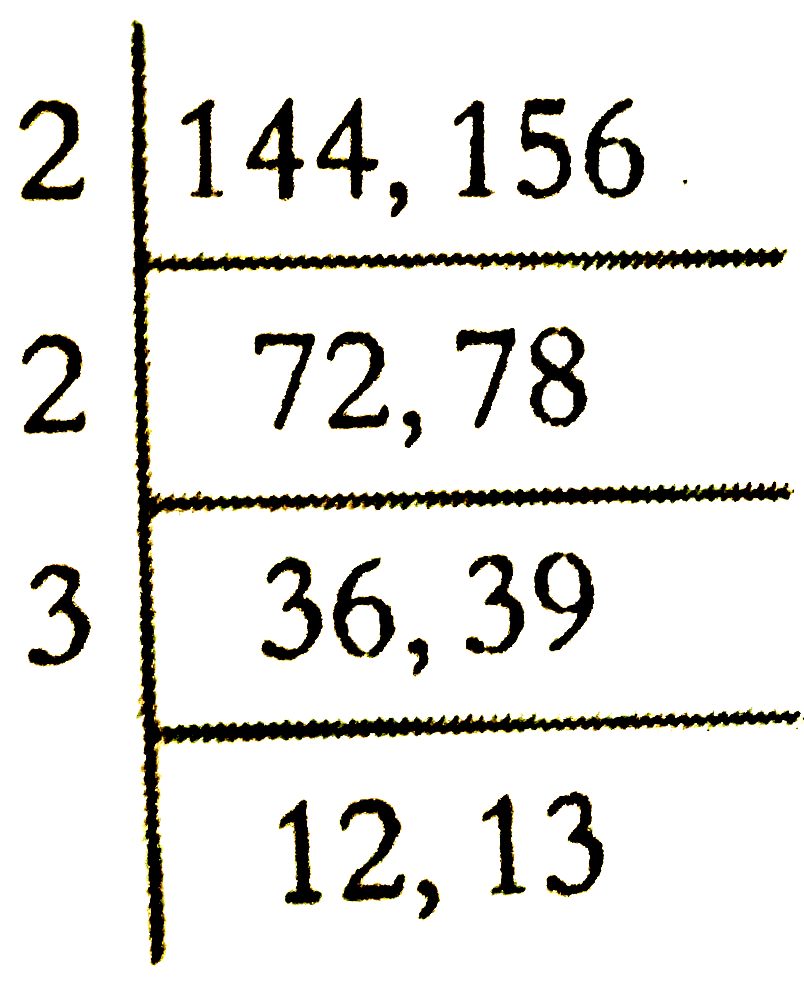
View SolutionFind the LCM of 160, 170 and 90.
View SolutionFind the LCM of 48, 72 and 108.
View SolutionFind the LCM of 8,12 and 15.
View SolutionFind the LCM of 20, 25 and 30
View SolutionFind the LCM of 42, 63 and 231.
View Solution
