Draw the regular polygons with sides 5, 6, 7 and 8.
To draw the regular polygons with sides 5, 6, 7, and 8, follow these steps:
1. Identify the Names of the Polygons:
- For 5 sides: This is called a Pentagon.
- For 6 sides: This is called a Hexagon.
- For 7 sides: This is called a Heptagon.
- For 8 sides: This is called an Octagon.
2. Draw a Regular Pentagon:
- Start by drawing a straight line for one side.
- Use a compass to measure the length of the side.
- From each endpoint of the line, draw two lines at an angle of 108° (the internal angle of a regular pentagon) to meet at a point.
- Ensure all sides are equal in length.
3. Draw a Regular Hexagon:
- Again, start with one side using a straight line.
- Use the compass to measure the same length as the side.
- From each endpoint, draw lines at an angle of 120° to meet at a point.
- Make sure all sides are equal in length.
4. Draw a Regular Heptagon:
- Begin with one side using a straight line.
- Measure the length of the side with a compass.
- From each endpoint, draw lines at an angle of approximately 128.57° to meet at a point.
- Ensure all sides are equal in length.
5. Draw a Regular Octagon:
- Start with one side using a straight line.
- Measure the length of the side with a compass.
- From each endpoint, draw lines at an angle of 135° to meet at a point.
- Ensure all sides are equal in length.
Summary of the Polygons:
- Pentagon: 5 equal sides
- Hexagon: 6 equal sides
- Heptagon: 7 equal sides
- Octagon: 8 equal sides
- For 5 sides: This is called a Pentagon.
- For 6 sides: This is called a Hexagon.
- For 7 sides: This is called a Heptagon.
- For 8 sides: This is called an Octagon.
- Start by drawing a straight line for one side.
- Use a compass to measure the length of the side.
- From each endpoint of the line, draw two lines at an angle of 108° (the internal angle of a regular pentagon) to meet at a point.
- Ensure all sides are equal in length.
- Again, start with one side using a straight line.
- Use the compass to measure the same length as the side.
- From each endpoint, draw lines at an angle of 120° to meet at a point.
- Make sure all sides are equal in length.
- Begin with one side using a straight line.
- Measure the length of the side with a compass.
- From each endpoint, draw lines at an angle of approximately 128.57° to meet at a point.
- Ensure all sides are equal in length.
- Start with one side using a straight line.
- Measure the length of the side with a compass.
- From each endpoint, draw lines at an angle of 135° to meet at a point.
- Ensure all sides are equal in length.
- Pentagon: 5 equal sides
- Hexagon: 6 equal sides
- Heptagon: 7 equal sides
- Octagon: 8 equal sides
Topper's Solved these Questions
- UNDERSTANDING ELEMENTARY SHAPES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - EXERCISE - SUBJECTIVE PROBLEMS (LONG ANSWER TYPE)
2 Videos
- UNDERSTANDING ELEMENTARY SHAPES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - EXERCISE - SUBJECTIVE PROBLEMS (INTEGER/NUMERICAL VALUE TYPE)
10 Videos
- UNDERSTANDING ELEMENTARY SHAPES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - EXERCISE - SUBJECTIVE PROBLEMS (VERY SHORT ANSWER TYPE)
10 Videos
- SYMMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Olympiad/HOTS Corner
13 Videos
- WHOLE NUMBERS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - WHOLE NUMBERS EXERCISE - OLYMPIAD/HOTS CORNER (FILL IN THE BLANKS)
5 Videos
Similar Questions
Consider a regular polygon with 10 sides, What is the number of triangles that can be formed by joining the vertices which have no common side with any of the sides of the polygon?
View SolutionRegular polygon a polygon is called a regular polygon if all its sides are equal and all its angles are equal.
View Solution
Knowledge Check
The interior angle of a regular polygon with n sides is 6 times that of an exterior angle of a regular polygon with 32 n sides. Then n equals
A12B20C10D18ABCDE is a regular pentagon with sides of length 6 cm. CD is also a side of a regular polygon with n sides. Given that ∠EDF=90∘, find n.
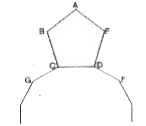 A18∘B10∘C20∘D12∘
A18∘B10∘C20∘D12∘The measure of each interior angle of a regular polygon with 8 sides is
A135∘B120∘C100∘D45∘
A circle of radius r is inscribed in a regular polygon with n sides (the circle touches all sides of the polygon). If the perimeter of the polygon is p, then the area of the polygon is
View SolutionDraw the net of a regular tetrahedron with side 6 cm.
View SolutionThe number of sides in two regular polygons are in the ratio 5:4 and the difference between each interior angle of the polygons is 6∘. Then the number of sides are.
View SolutionThere are two regular polygons with number of sides equal to (n−1)and(n+2). Their exterior angles differ by 6∘. The value of n is
View SolutionIn the two regular polygon number of sides are in the ratio 5:4 if difference betweeen their internal angles is 6∘ then number of sides in the polygon is
View Solution
