Draw a right angle and construct its bisector.
The correct Answer is:∠QOP
To solve the problem of drawing a right angle and constructing its bisector, follow these steps:
1. Draw a Horizontal Line:
- Start by drawing a horizontal line using a ruler. Label the endpoints as point O (the vertex of the angle) and point A (one endpoint of the line).
Hint: Use a ruler to ensure your line is straight.
2. Construct a Right Angle:
- At point O, use a protractor to measure a 90-degree angle. Mark this point as point B. Alternatively, you can use a compass to create a semicircle from point O, and then find the perpendicular line.
Hint: If using a compass, remember that the semicircle should be drawn with the center at point O.
3. Draw the Right Angle:
- Connect point O to point B with a straight line. Now you have a right angle ∠AOB.
Hint: Ensure that the angle is exactly 90 degrees for it to be a right angle.
4. Find the Bisector:
- To construct the bisector of the right angle, place the compass pointer on point O and draw an arc that intersects both lines OA and OB. Label the intersection points as C and D.
Hint: Make sure the compass width is the same when drawing arcs from point O to points C and D.
5. Draw Arcs from Points C and D:
- Without changing the compass width, place the compass pointer on point C and draw an arc above the angle. Then, place the compass pointer on point D and draw another arc that intersects the first arc. Label the intersection point of these arcs as point E.
Hint: The arcs should intersect above the angle to form the bisector.
6. Draw the Bisector Line:
- Use a ruler to draw a straight line from point O through point E. This line OE is the bisector of the right angle ∠AOB.
Hint: Ensure that the line passes through point O and point E to accurately represent the bisector.
Final Result:
You have successfully drawn a right angle ∠AOB and constructed its bisector OE.
- Start by drawing a horizontal line using a ruler. Label the endpoints as point O (the vertex of the angle) and point A (one endpoint of the line).
- At point O, use a protractor to measure a 90-degree angle. Mark this point as point B. Alternatively, you can use a compass to create a semicircle from point O, and then find the perpendicular line.
- Connect point O to point B with a straight line. Now you have a right angle ∠AOB.
- To construct the bisector of the right angle, place the compass pointer on point O and draw an arc that intersects both lines OA and OB. Label the intersection points as C and D.
- Without changing the compass width, place the compass pointer on point C and draw an arc above the angle. Then, place the compass pointer on point D and draw another arc that intersects the first arc. Label the intersection point of these arcs as point E.
- Use a ruler to draw a straight line from point O through point E. This line OE is the bisector of the right angle ∠AOB.
You have successfully drawn a right angle ∠AOB and constructed its bisector OE.
Topper's Solved these Questions
- PRACTICAL GEOMETRY BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS) (LEVEL-1)
30 Videos
- PRACTICAL GEOMETRY BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS) (LEVEL-2)
5 Videos
- PRACTICAL GEOMETRY BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - NCERT SECTION (EXERCISE 14.5)
10 Videos
- PLAYING WITH NUMBERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - OLYMPIAD/HOTS CORNER
18 Videos
- PREP TEST BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PREP TEST EXERCISE - SECTION-B
38 Videos
Similar Questions
Knowledge Check
In a right angled triangle ABC, the bisector of the right angle C divides AB into segment x and y and tan(A−B2)=t, then x:y is equal to
A(1+t)=(1−t)B(1−t):(t+1)C1:(1+t)D(1−t):1
Draw an angle of measure 147∘ and construct its bisector.
View SolutionTriangle ABC is right angles at B. Internet bisectors of acute angles A and C meet at point I. Find the measure of angle AIC
View SolutionDraw a line segment of length 9.5 cm and construct its perpendicular bisector.
View SolutionDraw an angle of 60∘. Draw its bisector.
View SolutionDraw a right triangle ABC . Use RHS condition to construct another triangle congruent to it.
View SolutionDraw an acute angle POQ and draw its line symmetry.
View SolutionIn the given figure, AD is bisector of angle ∠CAB and BD is bisector of ∠CBF. If the angle at C is 34∘, the angle ∠ADB is:
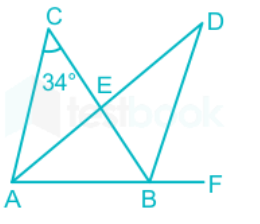
View Solution
