A _____ is a simple closed curve, all of whose points are at the same distance from a fixed point.
Diameter
Radius
Triangle
Circle
The correct Answer is:D
Step-by-Step Solution:
1. Understanding the Definition: We need to identify a simple closed curve where all points are equidistant from a fixed point.
2. Identifying Key Terms:
- A simple closed curve is a curve that starts and ends at the same point without crossing itself.
- The fixed point is the center of the curve.
- The distance from the fixed point to any point on the curve is constant and is known as the radius.
3. Visualizing the Curve: Imagine a point in the center (the fixed point) and draw a curve around it such that every point on the curve is the same distance from this center point.
4. Recognizing the Shape: The only shape that fits this description is a circle. A circle is defined as the set of all points in a plane that are a fixed distance (the radius) from a central point.
5. Final Answer: Therefore, the answer to the question is that the shape described is called a circle.
---
- A simple closed curve is a curve that starts and ends at the same point without crossing itself.
- The fixed point is the center of the curve.
- The distance from the fixed point to any point on the curve is constant and is known as the radius.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS) (LEVEL-2)5videos
PRACTICAL GEOMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - EXERCISE(MATCHING)1videos
PRACTICAL GEOMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - NCERT SECTION (EXERCISE 14.6)14videos
PRACTICAL GEOMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - OLYMPIAD/HOTS CORNER18videos
PLAYING WITH NUMBERS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PREP TEST EXERCISE - SECTION-B38videos
PREP TEST
Similar Questions
Circle is the set of all those points in a plane whose distance from a fixed point remains constant.
View SolutionTo find the equation of the hyperbola from the definition that hyperbola is the locus of a point which moves such that the difference of its distances from two fixed points is constant with the fixed point as foci
View Solution
Knowledge Check
- Question 1 - Select One
The locus of the point, the sum of the squares of whose distances from n fixed points Ai(xi,yi),i=1,2,…,n is equal t k2 is a circle
Apassing through the originBwith centre at the originCwith cnetre at the point of mean position of the given pointsDnone of these - Question 2 - Select One
The locus of the point, the sum of the squares of whose distances from n fixed points Ai(xi,yi),i=1,2,…,n is equal t k2 is a circle
Apassing through the originBwith centre at originCwith centre at a point of mean position of the given pointsDNone of these - Question 3 - Select One
A simple closed curve does not cross itself and its ends are joined.
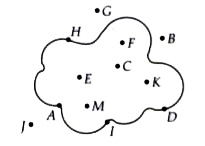
How many points lie in the exterior of the given curve?A2B3C4D5
A point P lying inside the curve y=√2ax−x2 is moving such that its shortest distance from the curve at any position is greater than its distance from X-axis. The point P enclose a region whose area is equal to
View SolutionThe locus of the point which moves such that the ratio of its distance from two fixed point in the plane is always a constant k(< 1) is
View SolutionOn the set of all points in a plane, the relation defined by the phrase 'at the same distance from the origin' is an equivalence relation.
View SolutionA polygon is a simple closed curve made up of only __________.
View SolutionA simple closed curve does not cross itself and its ends are joined.

.How many points lie in the interior of the curve?View Solution

