If AB = 4.8 cm and CD = 2.8 cm, construct a line segment whose length is AB-CD.
To solve the problem of constructing a line segment whose length is AB−CD, where AB=4.8cm and CD=2.8cm, we can follow these steps:
1. Calculate the Length of the Line Segment:
- First, we need to find the difference between AB and CD.
- AB−CD=4.8cm−2.8cm=2.0cm.
2. Gather Materials:
- You will need a ruler, a pencil, and a compass (if necessary).
3. Draw a Base Line:
- Using the ruler, draw a straight line on the paper. This will serve as the base for your line segment.
4. Mark the Starting Point:
- Choose a point on the line and label it as point A.
5. Measure the Length:
- Using the ruler, measure 2.0cm from point A along the line.
6. Mark the Endpoint:
- Mark the endpoint of the measurement and label it as point B.
7. Final Line Segment:
- The line segment AB is now constructed, and its length is 2.0cm.
Conclusion:
You have successfully constructed a line segment AB with a length of 2.0cm.
---
- First, we need to find the difference between AB and CD.
- AB−CD=4.8cm−2.8cm=2.0cm.
- You will need a ruler, a pencil, and a compass (if necessary).
- Using the ruler, draw a straight line on the paper. This will serve as the base for your line segment.
- Choose a point on the line and label it as point A.
- Using the ruler, measure 2.0cm from point A along the line.
- Mark the endpoint of the measurement and label it as point B.
- The line segment AB is now constructed, and its length is 2.0cm.
You have successfully constructed a line segment AB with a length of 2.0cm.
Topper's Solved these Questions
- PRACTICAL GEOMETRY BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - EXERCISE (SUBJECTIVE PROBLEMS) (SHORT ANSWER TYPE )
5 Videos
- PRACTICAL GEOMETRY BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - EXERCISE (SUBJECTIVE PROBLEMS) (LONG ANSWER TYPE )
5 Videos
- PRACTICAL GEOMETRY BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRY EXERCISE - EXERCISE (ASSERTION & REASON TYPE)
2 Videos
- PLAYING WITH NUMBERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - OLYMPIAD/HOTS CORNER
18 Videos
- PREP TEST BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PREP TEST EXERCISE - SECTION-B
38 Videos
Similar Questions
Draw line segments AB and CD of lengths 5.5 cm and 2.5 cm respectively. Construct a segment whose length equals 3¯¯¯¯¯¯AB−4¯¯¯¯¯¯CD.
View SolutionGiven ¯¯¯¯¯¯AB of length 7.3 cm and ¯¯¯¯¯¯CD of length 3.4 cm, construct a line segment ¯¯¯¯¯¯XY such that the length of ¯¯¯¯¯¯XY is equal to the difference beetween the lengths of ¯¯¯¯¯¯ABand¯¯¯¯¯¯CD. Verify by measurement.
View Solution
Knowledge Check
Let ABC be an acute angled triangle and CD be the altitude through C. If AB = 8 cm and CD = 6 cm, then the distance between the midpoints AD and BC is :
A6B4C4.5D5Two chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?A15.8 cmB12 cmC14 cmD14.6 cmQuadrilateral ABCD circumscribes a circle. If AB = 8 cm, BC = 7 cm and CD = 6 cm, then the length of AD is:
A7 cmB6.8 cmC7.5 cmD6 cm
With the help of a ruler construct line segment AB of length
7.8 cm
View SolutionWith the help of a ruler construct line segment AB of length
6.4 cm
View SolutionGiven two line segments AB and CD with measure 4.2 cm . Now draw a line segment of length equal to sum of line segment AB and CD.
View SolutionIn the figure, O is the centre of the circle of radius 29 cm, OP⊥AB,OQ⊥CD and AB is parallel to CD. If AB = 40 cm and CD = 42 cm, then the length of PQ is:
दी गयी आकृति में, O वृत्त का केंद्र है जिसकी त्रिज्या 29 सेमी है ,OP⊥AB,OQ⊥CD और AB, CD के समान्तर है। यदि AB= 40 सेमी और CD = 42 सेमी है, तो PQ की लंबाई है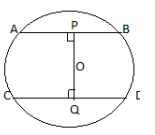
View SolutionConstruct a line segment AB = 8.9 cm. Construct another segment AC such that C lies on AB and AC = 3.8 cm. Measure the length of the remaining line segment.
View Solution
