A figure has a rotational symmetry of order more than 1, the angle of rotation can be
21∘
22∘
23∘
24∘
The correct Answer is:D
To solve the question regarding the angle of rotation for a figure with a rotational symmetry of order more than 1, we can follow these steps:
1. Understanding Rotational Symmetry:
- A figure has rotational symmetry if it can be rotated around a central point and still look the same at certain angles. The order of rotational symmetry refers to how many times the figure looks the same in one complete turn (360 degrees).
2. Identifying the Order:
- If a figure has a rotational symmetry of order more than 1, it means that there are multiple angles at which the figure can be rotated and still appear unchanged.
3. Calculating the Angle of Rotation:
- The angle of rotation can be calculated using the formula:
Angle of rotation=360∘n
where n is the order of symmetry.
4. Determining Possible Values:
- Since the order is more than 1, n can be any integer greater than 1 (e.g., 2, 3, 4, 5, etc.).
- The angle of rotation will thus be:
- For n=2: 360∘2=180∘
- For n=3: 360∘3=120∘
- For n=4: 360∘4=90∘
- For n=5: 360∘5=72∘
- And so on.
5. Conclusion:
- The angle of rotation can be any divisor of 360 degrees that corresponds to an integer greater than 1. Therefore, the possible angles of rotation can be 180°, 120°, 90°, 72°, etc.
- A figure has rotational symmetry if it can be rotated around a central point and still look the same at certain angles. The order of rotational symmetry refers to how many times the figure looks the same in one complete turn (360 degrees).
- If a figure has a rotational symmetry of order more than 1, it means that there are multiple angles at which the figure can be rotated and still appear unchanged.
- The angle of rotation can be calculated using the formula:
Angle of rotation=360∘n
where n is the order of symmetry.
- Since the order is more than 1, n can be any integer greater than 1 (e.g., 2, 3, 4, 5, etc.).
- The angle of rotation will thus be:
- For n=2: 360∘2=180∘
- For n=3: 360∘3=120∘
- For n=4: 360∘4=90∘
- For n=5: 360∘5=72∘
- And so on.
- The angle of rotation can be any divisor of 360 degrees that corresponds to an integer greater than 1. Therefore, the possible angles of rotation can be 180°, 120°, 90°, 72°, etc.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Exercise (Match the following)1videos
SYMMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Exercise (Very Short Answer Type)10videos
SYMMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - NCERT SECTION (Exercise -13.3)7videos
SYMMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SIMPLE EQUATIONSEXERCISE - Olympiad /Hots Corner18videos
SIMPLE EQUATIONS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - THE TRIANGLE AND ITS PROPERTIES EXERCISE - Olympiad/Hots Corner20videos
THE TRIANGLE AND ITS PROPERTIES
Similar Questions
Knowledge Check
- Question 1 - Select One
A square has a rotational symmetry of order
A1B2C3D4 - Question 2 - Select One
Which of the following letters has rotational symmetry of order more than 1 but not any line of symmetry?
AXBSCBDT - Question 3 - Select One
Which has no rotation of symmetry ?
AhexagonalBOrthochromicCCubicDTriclinic
The given figure has rotational symmetry of order
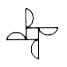 View Solution
View SolutionState whether the figure shows rotational symmetry. If yes then what is the order of rotational symmetry?
 View Solution
View SolutionShow that each of the letters H,I,N,S,X and Z has a rotational symmetry of order 2. Also, mark the point of rotational symmetry in each case.
View SolutionDraw, wherever possible, a rough sketch of:
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.View SolutionDraw a rough sketch of a quadrilateral with a rotational symmetry of order more than 1 but no line of symmetry.
View Solution

