PQRS is a kite.If ∠P=70∘ and ∠S=90.5∘,then ∠R equals
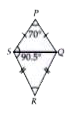
99∘
91∘
111∘
109∘
Step by step video & image solution for PQRS is a kite.If /_P=70^(@) and /_S=90.5^(@),then /_R equals by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-2 MATCH THE FOLLOWING)
1 Videos
- UNDERSTANDING QUADRILATERALSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-2 ASSERTION AND REASON TYPE)
5 Videos
- UNDERSTANDING QUADRILATERALSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-1)
35 Videos
- SQUARES AND SQUARE ROOTSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - Olympiad/HOTS Corner
20 Videos
- VISUALISING SOLID SHAPESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - VISUALISING SOLID SHAPESEXERCISE - OLYMPIAD/HOTS CORNER
10 Videos
Similar Questions
Knowledge Check
PQRS is a kite. ∠P=70∘,∠S=90.5∘,∠R equals
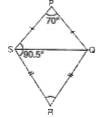 A99∘B91∘C111∘D109∘
A99∘B91∘C111∘D109∘ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC=70∘ , ∠BAC is 30∘ , find ∠ BCD. Further if AB=BC, find ∠ ECD.
AA. 80* and 50*BB. 30* and 80*CC. 100* and 70*DD. none of theseIf nPr=1680 and nCr=70, then n is equal to
A5B7C8D10
In a quadrilateral PQRS,∠P=70∘,∠Q=90∘,∠R=55∘. Find the measure of ∠S. What kind of quadrilateral is it convex or concave?
View SolutionIn ΔPQR it is given that = PQPR=QSSR. If ∠Q=70∘and∠R=50∘ then ∠QPS = ?
View SolutionIn a quadrilateral PQRS: ∠P=80∘,∠Q=90∘,∠R=65∘. Find the measure of ∠S. Is it a convex or concave quadrilateral?
View SolutionConstruct a quadrilateral PQRS in which PQ=3.5cm,QR=5cm, Rs=4.5cm, ∠Q=120∘ and ∠R=70∘.
View SolutionPQRS is a parallelogram in which
∠P=70∘,∠Q=90∘ and ∠R=100∘. How many points in the plane of the quadrilateral are there such that a point is equidistant from its vertices ?
View Solution
