Find the area of the hexagon in the adjoining figure, if ,
,
,
,
.
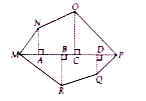
The correct Answer is:45.5 cm
Step by step video, text & image solution for Find the area of the hexagon in the adjoining figure, if MP = 9 cm, MD = 7 " cm", MC = 6 "cm", MB = 4" cm", MA = 2" cm", AN = 3" cm", OC = 5" cm", DQ =2" cm" and BR = 4" cm". by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Solved Examples21videos
MENSURATION
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - NCERT Section (Exercise 11.1)5videos
MENSURATION
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - Olympiad/HOTS Corner15videos
LINEAR EQUATIONS IN ONE VARIABLE
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - Olympiad/HOTS Corner6videos
PLAYING WITH NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, if AB = 10 cm, CD = 7 cm, SD = 4 cm and AS = 5 cm, then BC = ?
 A9 cmB8 cmC7.5 cmD6 cm
A9 cmB8 cmC7.5 cmD6 cm - Question 2 - Select One
Find the area of hexagon ABCDEF in which BL⊥AD,CM⊥AD,EN⊥AD and FP⊥AD such that AP=6cm,PL=2cm,LN=8cm,NM=2cm,MD=3cm,FP=8cm,EN=12cm,BL=8cm and CM=6cm.
 A200cm2B245cm2C234cm2D265cm2
A200cm2B245cm2C234cm2D265cm2 - Question 3 - Select One
In the adjoining figure, ∠AOB=90°,AC=BC,OA=10cmandOC=13cm.<br>.Theareaof<br>ΔAOB is
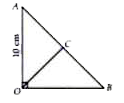 A120 cm2B135 cm2C140cm2D148 cm2
A120 cm2B135 cm2C140cm2D148 cm2
Find the area of the hexagon shown in Figure if MP=9cm, MD=7cm, MC=6cm, MB=4cm, MA=2cm, AN=3cm, OC=5cm, DQ=2cm and BR=4cm.
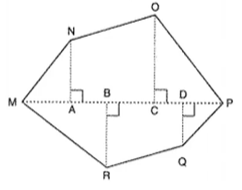 View Solution
View SolutionFind the area of the pentagon shown in Figure, if AD=10cm, AG=8cm, AH=6cm, AF=5cm, BF=5cm, CG=7cm and EH=3cm.
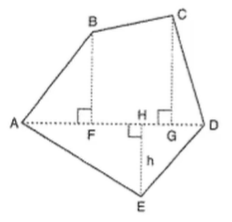 View Solution
View SolutionFind the area of pentagon ABCDE in which BL⊥AC,DM⊥AC and EN⊥AC such that AC = 18 cm, AM = 14 cm, AN = 6 cm, BL = 4 cm, DM = 12 cm and EN = 9 cm.
 View Solution
View SolutionFind the area of pentagone ABCDE in which BL⊥AC,CM⊥AD and EN⊥AD such that AC = 10 cm, AD = 12 cm, BL = 3 cm, CM = 7 cm and EN = 5 cm.
 View Solution
View SolutionFind the area of the pentagon ABCDE shown in Figure, if AD=8cm, AH=6cm, AG=4cm, AF=3cm, BF=2cm, CH=3cm and EG=2.5cm.
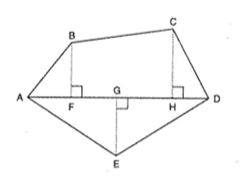 View Solution
View Solution


