The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs. 4.
The correct Answer is:Rs. 810
To solve the problem step by step, we will follow these instructions:
Step 1: Calculate the area of one rhombus tile.
The area A of a rhombus can be calculated using the formula:
A=12×d1×d2
where d1 and d2 are the lengths of the diagonals.
Given:
- d1=45cm
- d2=30cm
Substituting the values:
A=12×45×30
A=12×1350=675cm2
Step 2: Calculate the total area of 3000 tiles.
To find the total area of 3000 tiles, we multiply the area of one tile by the number of tiles:
Total Area=3000×675cm2
Total Area=2025000cm2
Step 3: Convert the total area from cm² to m².
To convert from cm² to m², we divide by 10,000 (since 1m2=10,000cm2):
Total Area in m2=202500010000=202.5m2
Step 4: Calculate the total cost of polishing the floor.
The cost of polishing per m² is Rs. 4. Therefore, the total cost can be calculated as:
Total Cost=Total Area in m2×Cost per m2
Total Cost=202.5×4=810Rs.
Final Answer:
The total cost of polishing the floor is Rs. 810.
---
The area A of a rhombus can be calculated using the formula:
A=12×d1×d2
where d1 and d2 are the lengths of the diagonals.
- d1=45cm
- d2=30cm
A=12×45×30
A=12×1350=675cm2
To find the total area of 3000 tiles, we multiply the area of one tile by the number of tiles:
Total Area=3000×675cm2
Total Area=2025000cm2
To convert from cm² to m², we divide by 10,000 (since 1m2=10,000cm2):
Total Area in m2=202500010000=202.5m2
The cost of polishing per m² is Rs. 4. Therefore, the total cost can be calculated as:
Total Cost=Total Area in m2×Cost per m2
Total Cost=202.5×4=810Rs.
The total cost of polishing the floor is Rs. 810.
Topper's Solved these Questions
- MENSURATIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - NCERT Section (Exercise 11.3)
10 Videos
- MENSURATIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - NCERT Section (Exercise 11.4)
10 Videos
- MENSURATIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - NCERT Section (Exercise 11.1)
5 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - MTG IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - Olympiad/HOTS Corner
15 Videos
- PLAYING WITH NUMBERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - Olympiad/HOTS Corner
6 Videos
Similar Questions
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45cm and 30cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs.4.
View SolutionThe sides of a triangle shaped sheet are 5cm, 12cm and 13cm. Find the cost of painting on the sheet at the rate of Rs 30 per cm2?
View Solution
Knowledge Check
If length of each side of a rhombus is 5 cm and length of one of its diagonal is 8 cm, find the length of other diagonal.
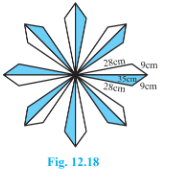
AA)5cmBB)6cmCC)7cmDD)8cmA floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9cm,28cm and 35cm (See figure). Find the cost polishing the tiles at the rate of 50 paise per cm2.
 ARs.790.60BRs.705.60CRs.675.60DRs.780.60
ARs.790.60BRs.705.60CRs.675.60DRs.780.60A sheet in the form of a rhombus whose diagonals are 10 m and 8 m. The cost of painting both of its surfaces at the rate of Rs 70 per m2 is
ARs 5600BRs 4000CRs 2800DRs 2000
Each side of a rhombus is 10cm. If one of its diagonals is 16cm find the length of the other diagonal.
View SolutionA floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9cm, 28cm and 35cm (See Figure). Find the cost of polishing the tiles at the rate of 50 paise per cm2 .

View SolutionA floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Fig. 12.18). Find the cost of polishing the tiles at the rate of 50p per cm2.
View SolutionThe side of a triangle shaped sheet are 5cm, 12cm and 13cm. Find the cost of painting on the sheet at the rate of Rs 30 per cm sq.
View SolutionEach side of a rhombus is 10 cm long and one of its diagonals measures 16 cm. Find the length of the other diagonal and hence find the area of the rhombus.
View Solution
