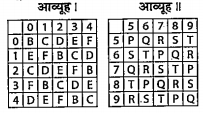
एक शब्द फेवल एक संख्या समूह द्वारा दर्शापा गया है जैसा कि विंकल्पों में से किसी एक में दिया गया है। जिकल्पों में दिए गए संख्या समूह, अक्षरों के दो वर्गों द्वारा दर्शाए गए हैं, जैस्षा कि नीचे दिए गए दो आच्यूहों.में हैं। आब्यूह 1 के स्तम्भों और पंवितयों को संख्या 0 से 4 तक दिया गया है और आब्यूंह II पर के रुतम्भों तथा गंक्टियों को 5 से 9 तक। इन आव्यूहों से एक अंक्षर को पहले उसकी पंक्ति | और फिर स्तम्भ संख्या द्वारा दर्शाया जा राकता | है। उदाहरण के लि 'D'को 02, 14 आदि ., द्वारा दर्शाया जा सफता है तथा गए 'R' को 57, 76, आदि द्वारा दर्शाया जा-सकता है। इसी तरह से आपको शब्द "BEST" के लिए संख्या समूह को पहचानना है।
एक शब्द फेवल एक संख्या समूह द्वारा दर्शापा गया है जैसा कि विंकल्पों में से किसी एक में दिया गया है। जिकल्पों में दिए गए संख्या समूह, अक्षरों के दो वर्गों द्वारा दर्शाए गए हैं, जैस्षा कि नीचे दिए गए दो आच्यूहों.में हैं। आब्यूह 1 के स्तम्भों और पंवितयों को संख्या 0 से 4 तक दिया गया है और आब्यूंह II पर के रुतम्भों तथा गंक्टियों को 5 से 9 तक। इन आव्यूहों से एक अंक्षर को पहले उसकी पंक्ति | और फिर स्तम्भ संख्या द्वारा दर्शाया जा राकता | है। उदाहरण के लि 'D'को 02, 14 आदि ., द्वारा दर्शाया जा सफता है तथा गए 'R' को 57, 76, आदि द्वारा दर्शाया जा-सकता है। इसी तरह से आपको शब्द

A

24,22,77,97

B

24,22,77,96

C

24,22,76,97

D

24,21,77,97

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for एक शब्द फेवल एक संख्या समूह द्वारा दर्शापा गया है जैसा कि विंकल्पों में से किसी एक में दिया गया है। जिकल्पों में दिए गए संख्या समूह, अक्षरों के दो वर्गों द्वारा दर्शाए गए हैं, जैस्षा कि नीचे दिए गए दो आच्यूहों.में हैं। आब्यूह 1 के स्तम्भों और पंवितयों को संख्या 0 से 4 तक दिया गया है और आब्यूंह II पर के रुतम्भों तथा गंक्टियों को 5 से 9 तक। इन आव्यूहों से एक अंक्षर को पहले उसकी पंक्ति | और फिर स्तम्भ संख्या द्वारा दर्शाया जा राकता | है। उदाहरण के लि 'D'को 02, 14 आदि ., द्वारा दर्शाया जा सफता है तथा गए 'R' को 57, 76, आदि द्वारा दर्शाया जा-सकता है। इसी तरह से आपको शब्द "BEST" के लिए संख्या समूह को पहचानना है। by Reasoning experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023
Class 14REASONINGआवयूह परीक्षण

Topper's Solved these Questions

Similar Questions