Arrange the following in order of increasing diameter, giving the approximate maximum diameter of each in appropriate units. An E. coli cell, a human red blood cell, a ribosome, an amoeba, a microtubule
To arrange the following biological entities in order of increasing diameter, we will first identify the approximate maximum diameter of each entity and then list them accordingly. The entities to arrange are: a ribosome, an E. coli cell, a human red blood cell, an amoeba, and a microtubule.
1. Identify the approximate diameters:
- Ribosome: The diameter of a ribosome is approximately 20-30 nanometers (nm).
- Microtubule: The diameter of a microtubule is about 25 nanometers (nm).
- E. coli cell: The diameter of an E. coli cell is approximately 0.5-2 micrometers (µm).
- Human red blood cell: The diameter of a human red blood cell is about 6-8 micrometers (µm).
- Amoeba: The diameter of an amoeba can vary significantly, but it is generally around 100-500 micrometers (µm).
2. Convert all measurements to the same unit for comparison:
- Ribosome: 20-30 nm = 0.020-0.030 µm
- Microtubule: 25 nm = 0.025 µm
- E. coli cell: 0.5-2 µm
- Human red blood cell: 6-8 µm
- Amoeba: 100-500 µm
3. Arrange the entities in order of increasing diameter:
- Ribosome: 0.020-0.030 µm
- Microtubule: 0.025 µm
- E. coli cell: 0.5-2 µm
- Human red blood cell: 6-8 µm
- Amoeba: 100-500 µm
4. Final Arrangement:
- Ribosome (0.020-0.030 µm)
- Microtubule (0.025 µm)
- E. coli cell (0.5-2 µm)
- Human red blood cell (6-8 µm)
- Amoeba (100-500 µm)
Summary of the Order:
1. Ribosome (0.020-0.030 µm)
2. Microtubule (0.025 µm)
3. E. coli cell (0.5-2 µm)
4. Human red blood cell (6-8 µm)
5. Amoeba (100-500 µm)
- Ribosome: The diameter of a ribosome is approximately 20-30 nanometers (nm).
- Microtubule: The diameter of a microtubule is about 25 nanometers (nm).
- E. coli cell: The diameter of an E. coli cell is approximately 0.5-2 micrometers (µm).
- Human red blood cell: The diameter of a human red blood cell is about 6-8 micrometers (µm).
- Amoeba: The diameter of an amoeba can vary significantly, but it is generally around 100-500 micrometers (µm).
- Ribosome: 20-30 nm = 0.020-0.030 µm
- Microtubule: 25 nm = 0.025 µm
- E. coli cell: 0.5-2 µm
- Human red blood cell: 6-8 µm
- Amoeba: 100-500 µm
- Ribosome: 0.020-0.030 µm
- Microtubule: 0.025 µm
- E. coli cell: 0.5-2 µm
- Human red blood cell: 6-8 µm
- Amoeba: 100-500 µm
- Ribosome (0.020-0.030 µm)
- Microtubule (0.025 µm)
- E. coli cell (0.5-2 µm)
- Human red blood cell (6-8 µm)
- Amoeba (100-500 µm)
1. Ribosome (0.020-0.030 µm)
2. Microtubule (0.025 µm)
3. E. coli cell (0.5-2 µm)
4. Human red blood cell (6-8 µm)
5. Amoeba (100-500 µm)
Topper's Solved these Questions
- BOOK - CENGAGE BIOLOGYCHAPTER - CEL: THE BASIC UNIT OF LIFEEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES9videos
CEL: THE BASIC UNIT OF LIFE
- BOOK - CENGAGE BIOLOGYCHAPTER - BIOLOGICAL CLASSIFICATION EXERCISE - CHALLENGING EXERCISE1videos
BIOLOGICAL CLASSIFICATION
- BOOK - CENGAGE BIOLOGYCHAPTER - CELL CYCLE AND CELL DIVISION EXERCISE - CHALLENGING EXERCISE6videos
CELL CYCLE AND CELL DIVISION
Similar Questions
For the following unit cell of a 2D arrangement what will be approximate void % ?
 View Solution
View SolutionAnswer the following:
a. Which of the following has density greater than water ? Li,Na,K,Cs.
b. Arrange K, Li, Rb in other of increasing electrode potential.
c. Arrange Na, Li, K and Cs in increasing order of metallic bond.
d. Which among Na, K, Cs and Li forms stable hydride ?
e. On reacting eith oxygen, potassium can form K2O, KO2 and K2O2. Is it correct ?
f. Give the name of the hardest alakli metal.
g. Arrange the following in order orf increasing polarising albility.
Li⊕,Na⊕,K⊕,Cs⊕
h. Mention some of the properties of alkali metals which increse down the group.
i. Mention some of the properties of alkali metals which decrease down the group.View Solution
Knowledge Check
- Question 1 - Select One
The human red blood cells are about ________in diameter.
A7.0μmB9.0μmC5.4μmD4.5μm - Question 2 - Select One
Which one of the following organs of the human body break down the old red blood cells and store iron from them?
AKidneyBGall bladderCPancreasDSpleen - Question 3 - Select One
A simple pendulum was given to a physics student to determine its time period. Arrange the following steps in sequential order to determine its time period.
(A). Calculate the radius of the bob 'R' by divding the diameter by 2.
(B) Take a metre scale and measure the length of the string from the point of suspension to the lower tip of the bob (l1)
(C). Place the bob over a meter scale and hold it in postion with two wooden blocks of stiff cadboards. Measure the diamter (D)of the bob.
(D). NOW, the length of the pendulum (l) is given by (l1−R)
E. Consider the formula T=2π.√lg calculate.
The time period of the simple pendulum.AABCDEBEDCBACBCADEDDEABC
Arrange the following statements in the correct order in which they occur during the formation and removal of urine in human beings.
(a) Ureters carry urine to the urinary bladder
(b) Wastes dissolved in water is filtered out as urine in the kidneys.
(c ) Urine stored in urinary bladder is passed out through the urinary opening at the end of the urethra
(d) Blood containing useful and harmful substances reaches the kidneys for filtration
(e ) Blood containing useful and harmful substances reaches the kidneys for filtration.View SolutionThe following table gives the length of three copper wires, their diameters, and the applied potential difference across their ends. Arrange the wires in increasing order according to the following:
The magnitude of the electric field within them.View SolutionThe following table gives the length of three copper wires, their diameters, and the applied potential difference across their ends. Arrange the wires in increasing order according to the following:
The drift speed of electrons through them, andView SolutionThe following table gives the length of three copper wires, their diameters, and the applied potential difference across their ends. Arrange the wires in increasing order according to the following:
The current density within them.
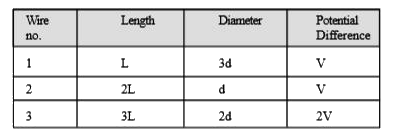 View Solution
View SolutionA simple pendulum was given to a physics student to determine its time period. Arrange the following steps in sequential order to determine its time period.
(A). Calculate the radius of the bob 'R' by divding the diameter by 2.
(B) Take a metre scale and measure the length of the string from the point of suspension to the lower tip of the bob (l1)
(C). Place the bob over a meter scale and hold it in postion with two wooden blocks of stiff cadboards. Measure the diamter (D)of the bob.
(D). NOW, the length of the pendulum (l) is given by (l1−R)
E. Consider the formula T=2π.√lg calculate.
The time period of the simple pendulum.View Solution

