The distance from the centre of the earth of the plane of Arctic Circle is 3700 miles (to the nearest 100 miles). The radius of the earth in 4000 miles. Find the radius of Arctic Circle.
Text Solution
The correct Answer is:1487
|
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (LEVEL 3)
8 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (MULTIPLE CHOICE QUESTION)
24 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (LEVEL 1)
10 Videos
- ALGEBRAIC EXPRESSIONS AND POLYNOMIALS BOOK - CENGAGECHAPTER - ALGEBRAIC EXPRESSIONS AND POLYNOMIALS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- LAWS OF EXPONENTS AND LOGARITHMS BOOK - CENGAGECHAPTER - LAWS OF EXPONENTS AND LOGARITHMS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
Knowledge Check
At what distance from the centre of the earth, the value of acceleration due to gravity g will be half that on the surface ( R = radius of earth)
A2RBRC1.414RD0.414RFrom a point Q, the length of the tangent to a circle is 12 cm and the distance of Q from the centre is 13 cm. The radius of the circle is 13 cm. The radius of the circle is :
A12 cmB13 cmC5 cmDNone of theseFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :
A7 cmB12 cmC15 cmD24.5 cm
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
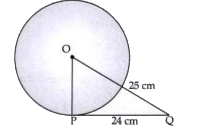
View SolutionThe distance of geostationary satellite from the centre of the earth (radius R) is nearest to
View SolutionOne goes from the centre of the earth to a distance two third the radius of the earth. The acceleration due to gravity is highest at
View SolutionFrom a point A, the length of the tangent to ta circle is 24 cm . And the distance of a from the centre is 25 cm . The radius of the circle is
View SolutionThe distance of geostationary satellite from the centre of the earth (radius R) is nearest to
View Solution
