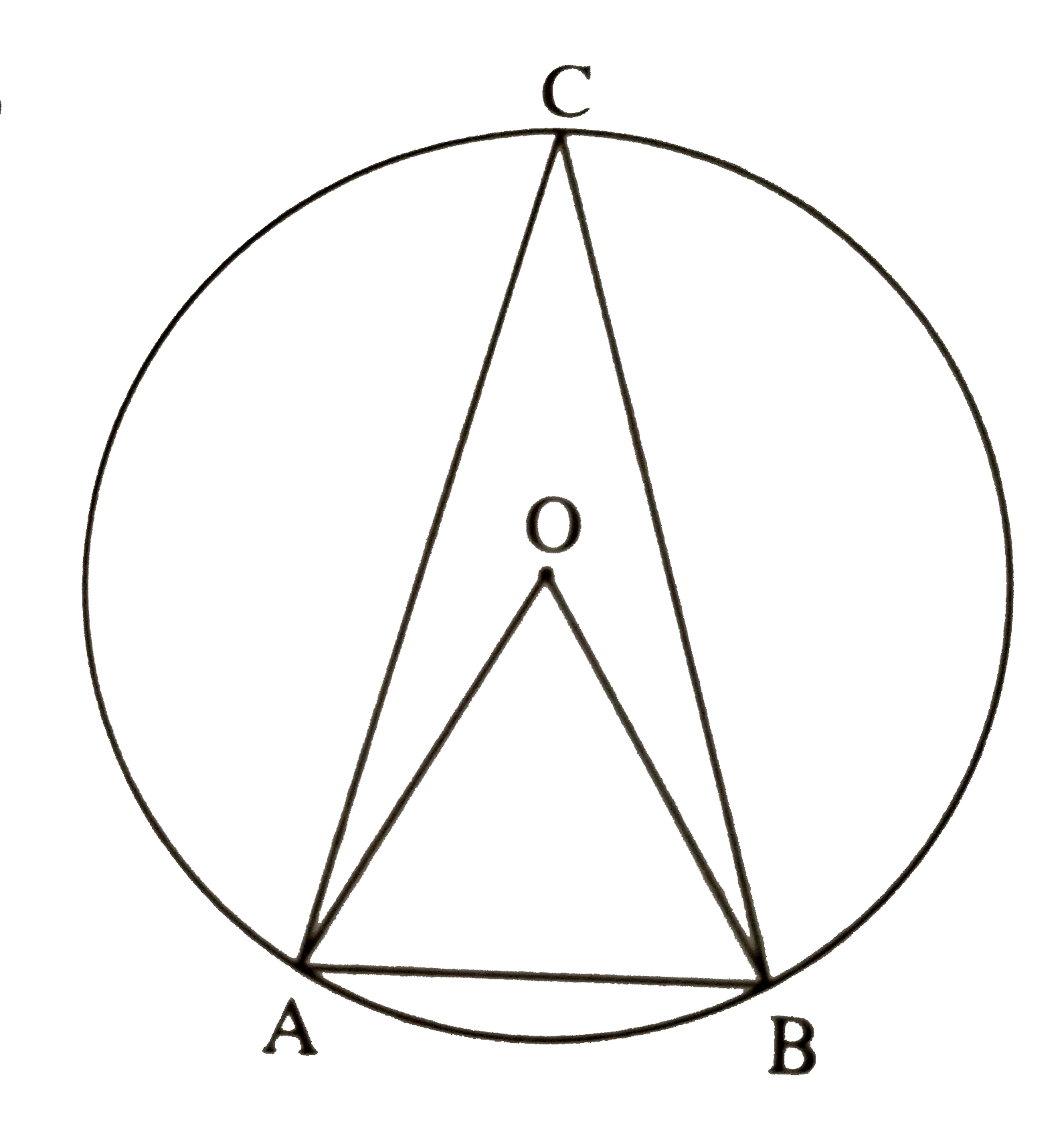
If the length of a chord AB is equal to the radius OA of the circle, then $∠ A B O$ equals (O is the center)

A

$120^{\circ}$

B

$60^{\circ}$

C

$45^{\circ}$

D

$30^{\circ}$

Text Solution

Verified by Experts

The correct Answer is:B

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Topper's Solved these Questions

BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (MULTIPLE CHOICE QUESTION)
24videos
CIRCLES
BOOK - CENGAGECHAPTER - ALGEBRAIC EXPRESSIONS AND POLYNOMIALS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10videos
ALGEBRAIC EXPRESSIONS AND POLYNOMIALS
BOOK - CENGAGECHAPTER - LAWS OF EXPONENTS AND LOGARITHMS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10videos
LAWS OF EXPONENTS AND LOGARITHMS

Similar Questions

Knowledge Check

Question 1 - Select One
If the length of a chord of a circle is equal to that of the radius of the circle , then the angle subtended , in radians , at the centre of the circle by the chord is
A1
B $\frac{π}{2}$
C $\frac{π}{3}$
D $\frac{π}{4}$
Question 2 - Select One
The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to :
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$
Question 3 - Select One
The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$

CENGAGE-CIRCLES-OLYMPIAD AND NTSE LEVEL EXERCISES

Home
Ask Doubt
Profile