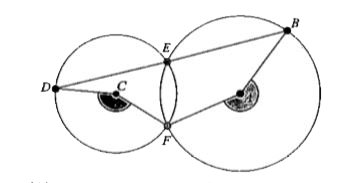
In the figure , A and C are the centres of the circles. DEB is a straight line. If relex angle BAF = 208∘ then obtuse angle DCF=
A
152∘
B
176∘
C
120∘
D
150∘
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- CIRCLES AND CYCLIC QUADRILATERALS BOOK - CENGAGECHAPTER - CIRCLES AND CYCLIC QUADRILATERALS EXERCISE - TEST YOURSELF (MULTIPLE CHOICE QUESTIONS)
16 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - TEST YOURSELF (Multiple Choice Questions) OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- DETERMINANTSBOOK - CENGAGECHAPTER - DETERMINANTSEXERCISE - Puzziles and games
5 Videos
Similar Questions
Knowledge Check
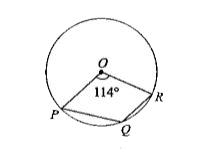
O is the centre of the circle, ABN is a straight line. Find ∠AOC.
 A128∘B132∘C130∘D135∘
A128∘B132∘C130∘D135∘In the figure, O is the centre of the circle . ∠PQR is equal to
 A57∘B63∘C123∘D92∘
A57∘B63∘C123∘D92∘In the given figure, O is the centre of the circle. ABD is a straight line and ∠CBD=65∘. Find reflex ∠AOC (marked x∘).
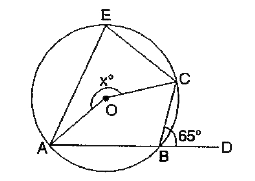 A130∘B230∘C190∘D65∘
A130∘B230∘C190∘D65∘
In the figure given alongside ,AB and CD are straight lines thorugh the centre O of a circle. If ∠AOC=80∘and∠CDE=40∘ , find ∠DCE
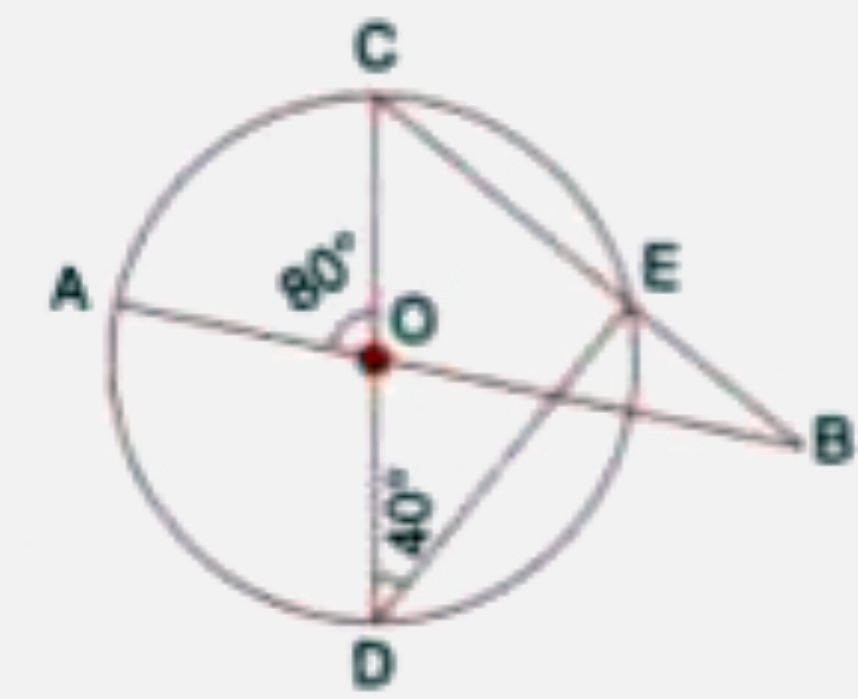
View SolutionIn the diagram, CB and CD are tangents to the circle with centre O. AOC is a straight line and ∠OCB=34∘.∠ABO equals.

View SolutionIn the given figure, O is the centre of the circle, ∠ACB=54∘ and BCF is a straight line. Find x.
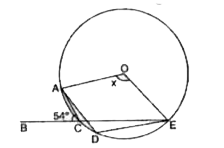
View SolutionIn the figure , O is the centre of the circle and BCD is tangent to it at C . Find the value of ∠BAC+∠ACD

View SolutionIn the given figure, RST is the tangent to the circle with centre O, at S. AOS is a straight line BO||RT and ∠ORS=46∘. Then ∠ BAC equals
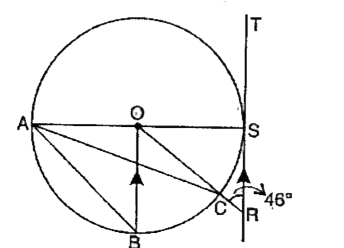
View Solution