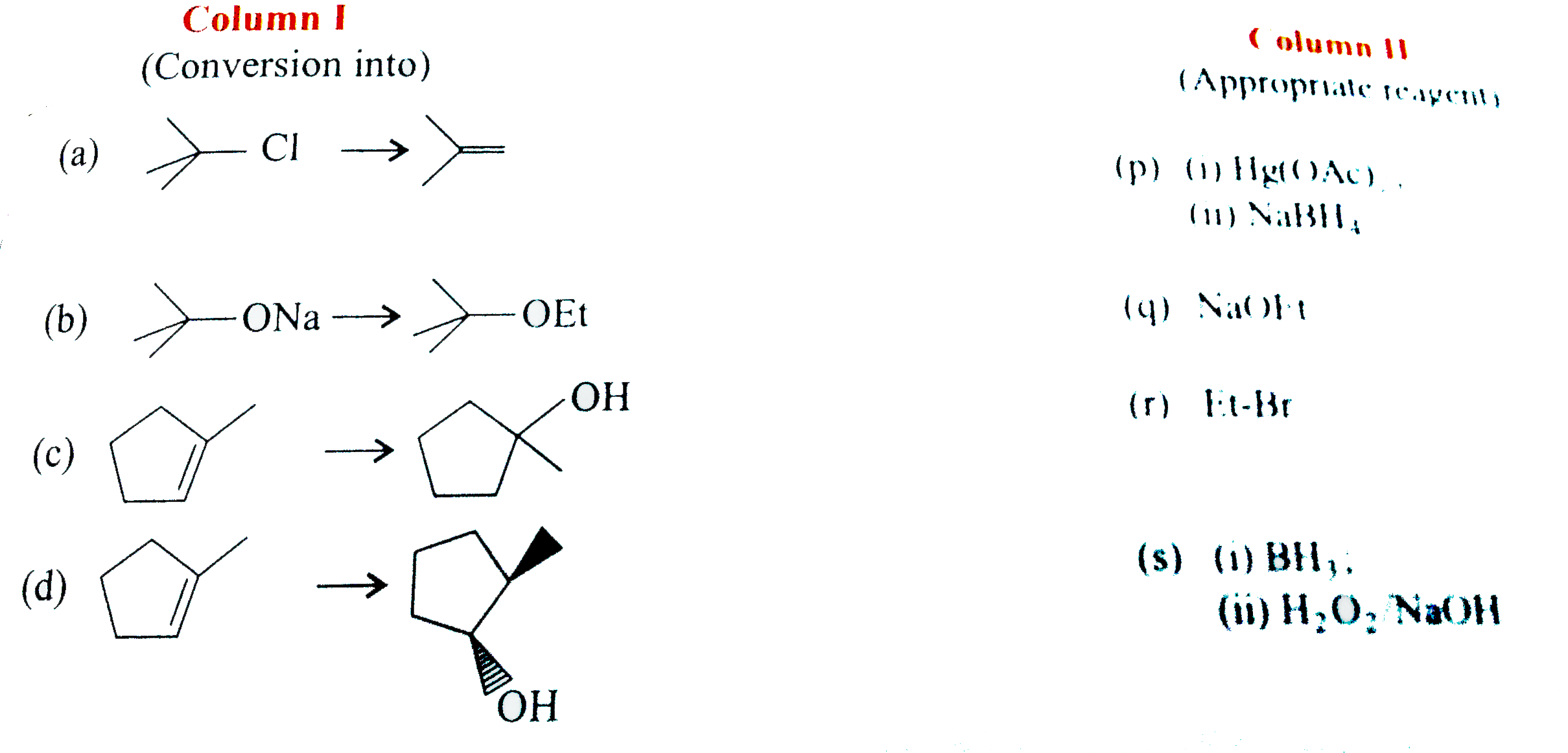
Match the following column.
AB(A)Work(p)kgm/s2(B)Force(q)m2(C)Speed(r)m/s(D)Area(s)kgm2/s2
A-s, B-p, C-r, D-q
A-p, B-s, C-r, D-q
A-s, B-r, C-p, D-q
A-s, B-p, C-q, D-r
To solve the problem of matching the physical quantities from column A to column B, we need to identify the dimensional formulas for each term in column A and match them with the appropriate terms in column B.
1. Identify the Dimensional Formula for Work (A):
- Work is defined as Force × Displacement.
- The dimensional formula for Force is MLT−2 (mass × acceleration).
- Displacement has a dimensional formula of L (length).
- Therefore, the dimensional formula for Work is:
Work=Force×Displacement=MLT−2×L=ML2T−2
- This corresponds to option (s) in column B.
2. Identify the Dimensional Formula for Force (B):
- As mentioned, Force is defined as mass times acceleration.
- The dimensional formula for Force is:
Force=MLT−2
- This corresponds to option (p) in column B.
3. Identify the Dimensional Formula for Speed (C):
- Speed is defined as distance traveled per unit time.
- The dimensional formula for Speed is:
Speed=DistanceTime=LT=LT−1
- This corresponds to option (r) in column B.
4. Identify the Dimensional Formula for Area (D):
- Area is defined as length squared.
- The dimensional formula for Area is:
Area=L2
- This corresponds to option (q) in column B.
Final Matching:
- A (Work) matches with (s).
- B (Force) matches with (p).
- C (Speed) matches with (r).
- D (Area) matches with (q).
Summary of Matches:
- A → s (Work → kg m²/s²)
- B → p (Force → kg m/s²)
- C → r (Speed → m/s)
- D → q (Area → m²)
- Work is defined as Force × Displacement.
- The dimensional formula for Force is MLT−2 (mass × acceleration).
- Displacement has a dimensional formula of L (length).
- Therefore, the dimensional formula for Work is:
Work=Force×Displacement=MLT−2×L=ML2T−2
- This corresponds to option (s) in column B.
- As mentioned, Force is defined as mass times acceleration.
- The dimensional formula for Force is:
Force=MLT−2
- This corresponds to option (p) in column B.
- Speed is defined as distance traveled per unit time.
- The dimensional formula for Speed is:
Speed=DistanceTime=LT=LT−1
- This corresponds to option (r) in column B.
- Area is defined as length squared.
- The dimensional formula for Area is:
Area=L2
- This corresponds to option (q) in column B.
- A (Work) matches with (s).
- B (Force) matches with (p).
- C (Speed) matches with (r).
- D (Area) matches with (q).
- A → s (Work → kg m²/s²)
- B → p (Force → kg m/s²)
- C → r (Speed → m/s)
- D → q (Area → m²)
Topper's Solved these Questions
- UNITS AND MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - MANDATORY EXERCISE (EXERCISE SET II) MULTIPLE-CHOICE QUESTIONS WITH ONE OR MORE THAN ONE CORRECT ANSWERS
4 Videos
- UNITS AND MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - MANDATORY EXERCISE (EXERCISE SET III)
12 Videos
- UNITS AND MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - MANDATORY EXERCISE (EXERCISE SET II) COMPREHENSION
1 Videos
- STATICSBOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
9 Videos
Similar Questions
Knowledge Check
Match the following:
Column-IColumn-II(P) R.M.S(1)23NKT(Q) PV(2)KT(R) Average K.E.(3)√3PVM(S) Most probable speed(4)√2RTMAPQRS1243BPQRS2143CPQRS3124DPQRS4123Column IColumn IIColumn IIIColumn IVPhysical quantityMKS systemCGS systemFPS system(A)Length(a)newton(p)erg(1)poundal(B)Mass(b)m(q)dyne(2)ft-poundal(C)Force(c)kg(r)erg/s(3)ft(D)Power(d)joule(s)g(4)lb(E)Work(e)watt(t)cm(5)ft-poundal/s
A0∘B45∘C60∘D90∘
Match the following.
Column AColumn B(A)Area/length( )(a)metre−1(B)Mass/volume( )(b)No unit(C)Length/area( )(c)metre(D)Length2/area( )(d)kg m−3
View SolutionMatch the following :
Column-IColumn-II(A)3s1(p)n=3(B)3p1(q)l=0(C)4s1(r)l=1(D)4d1(s)m=0(t)m=±1
View SolutionIn the figure shown, the coefficient of friction between the two blocks is 0.1 and coefficient of friction between the block B and ground is 0.2, masses of A and B are 20kg and 40kg respectively. where aA= acceleration of A and aB= acceleration of B.
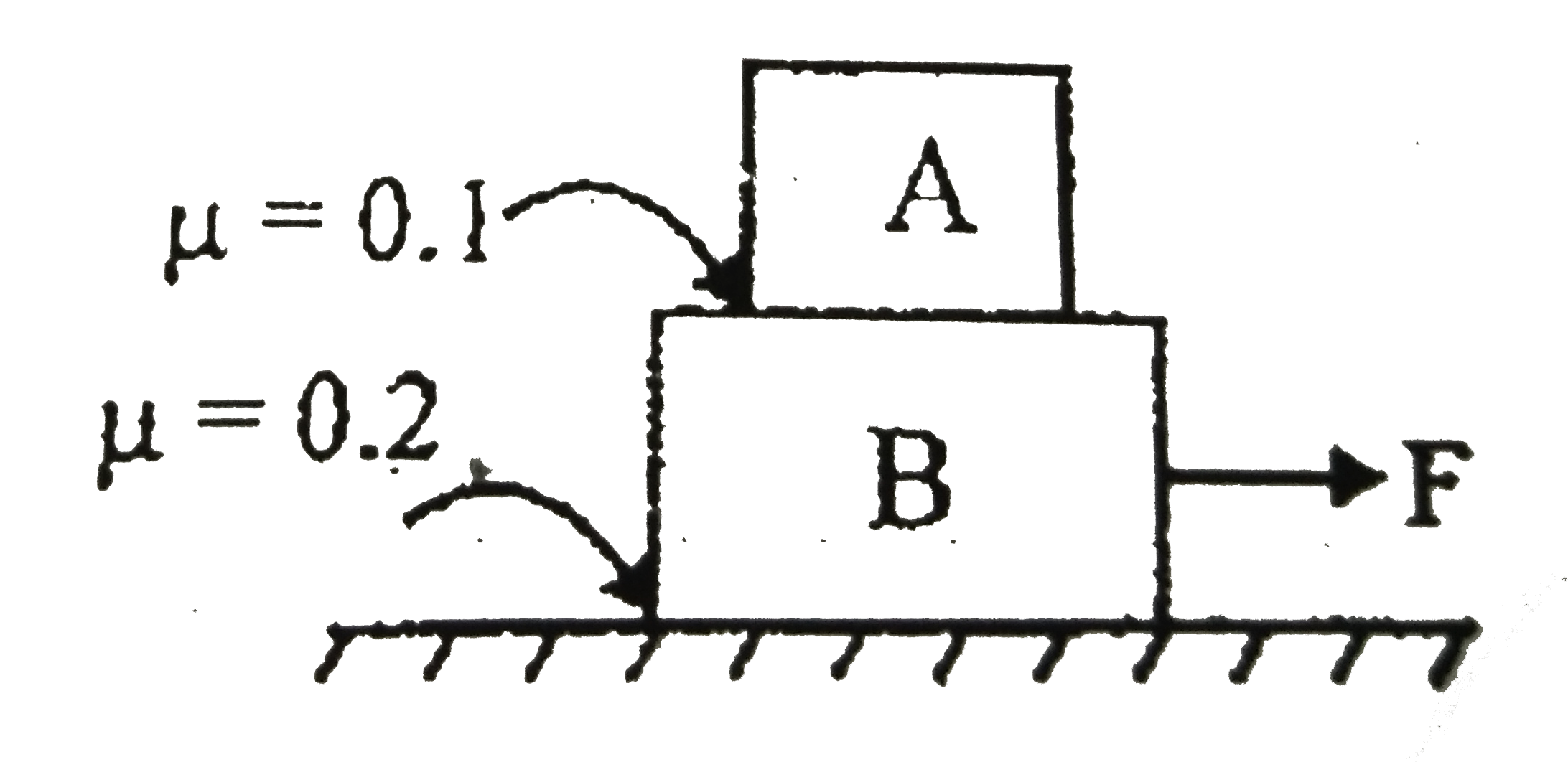
Column IColumn II(A)F=50N(P)aA=0m/s2(B)F=150N(Q)aA=0.5m/s2(C)F=200N(R)aB=0.5m/s2(S)aB=1.5m/s2
View SolutionQ is energy released in the decay m_(x) is atomic mass of parent nucleus m_(y) is atomic mass of daughter nucleus and m_(e) is mass of elctron then match the following:
Column-IColumn-II(A)k capture(P)Q=(mx−my)c2(B)β−decay(Q)Q=(mx−my−mc)c2(C)β+decay(R)Q=(mx−my−2me)c2(S)Q=(mx−my+2me)c2
View Solution1 kg m/s2 =___gm-mm/s2
View SolutionA balloon rises up with constant net acceleration of 10m/s2. After 2 s a particle drops from the balloon. After further 2 s match the following : (Takeg=10m/s2)
Column IColumn II(A)Height of perticle from ground(p)Zero(B)Speed of particle(q)10SIunits(C)Displacement of Particle(r)40SIunits(D)Acceleration of particle(s)20SIunits
View Solution