Question

Use the principle of mathematical induction to show that $5^{2n+1}+3^{n+2}{.2}^{n-1}$ divisible by 19 for all natural numbers n.

Explanation

Let `P(n)=5^(2n+1)+3^(n+2).2^(n-1)`
Step I For `n=1,P(1)=5^(2+1)+3^(1+2).2^(1-1)=125+27=152`, which is divisible by 19.
Step II Assume that the result is true for `n=k`, i.e.,
`P(k)=5^(2k+1)+3^(k+2).2^(k-1)` is divisible by 19.
`rArr P(k)=19r`, where r is an integer .
Step III for `n=k+1`.
`P(k+1)=5^(2(k+1)+1)+3^(k+1+2).2^(k+1-1)`
`5^(2k+3)+3^(k+3).2^(k)`
`=25.5^(2k+1)+3.3^(k+2).2.2^(k-1)`
`=25.5^(2k+1)+6.3^(k+2).2^(k-1)`

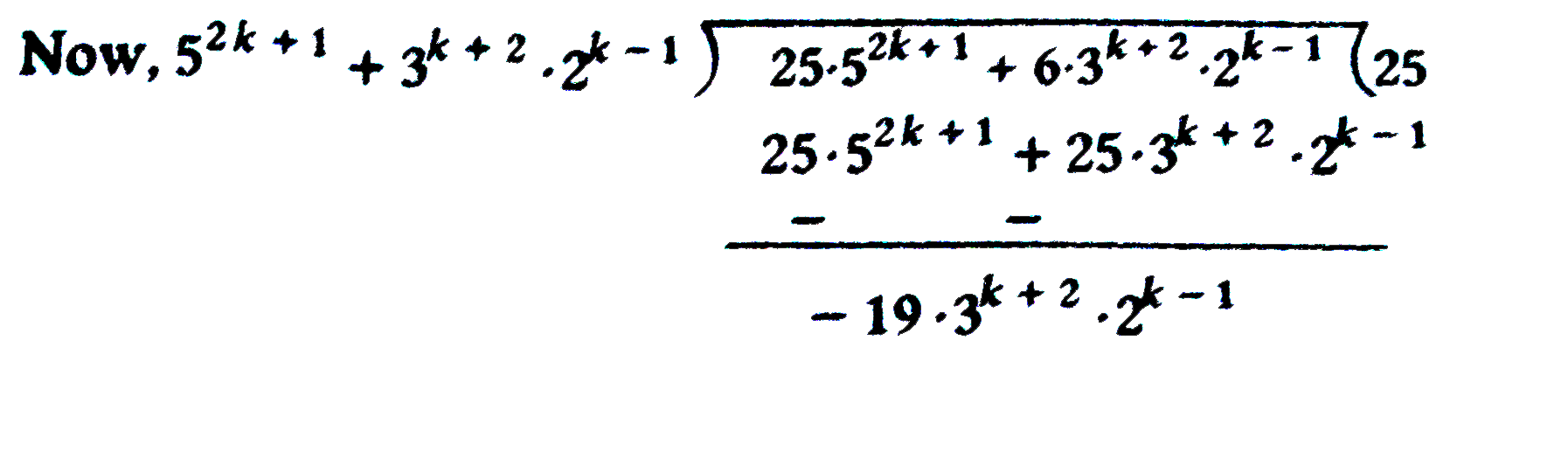
`therefore 25.56(2k+1)+6.3^(k+2).2^(k-1)=25.(5^(2k+1)+3^(k-2).2^(k-2))-19.3^(k+2).2^(k-1)`
i.e., `P(k+1)=25P(k)-19.3^(k+2).2^(k-1)`
But we know that P(k) is divisible by 19. Also , `19.3^(k+2).2^(k-1)` is clearly divisible by 19.
Therefore , `P(k+1)` is divisible by 19. This shows that the result is true for `n=k+1`.
Hence , by the principle of mathematical induction , the result is true for all `n in N`.