If →a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5,|→c|=7, then angle between →a and →b is : a. π2 b. π3 c. π4 d. π6Solution in Punjabi
π2
π3
π4
π6
The correct Answer is:B
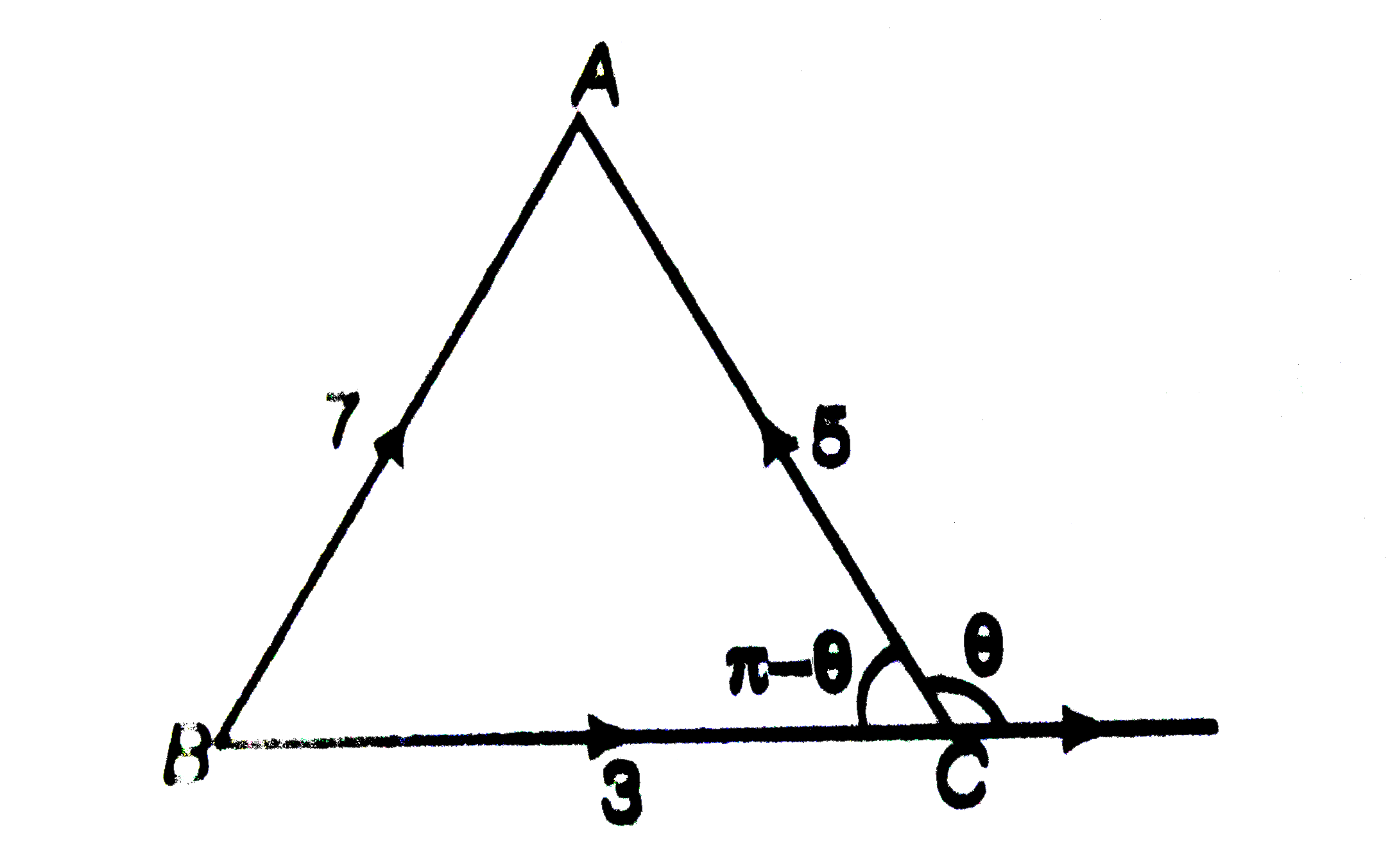
Let θ be the angle between a and b. then, ∠C=π−θ.
∴cos(π−θ)=32+52−722(3)(5)
∴−cosθ=−12
∴θ=60∘=π3
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 2
17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
Classify the following measure as scalar and vector: 10Kg
View SolutionIf a=2ˆi−ˆj+2ˆkandb=−ˆi+ˆj−ˆk, then find a+b. Also, find a unit vector along a+b.
View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
View SolutionIf →a+→b+→c=0,|→a|=3,∣∣→b∣∣=5,|→c|=7, then angle between →aand→b is (A) π6 (B) 2π3 (C) 5π3 (D) π3
View SolutionIf →a,→b,→c are unit vectors such that veca is perpendicular to →band→cand∣∣→a+→b+→c∣∣=1 then the angle between →band→c is (A) π2(B)pi(C)0(D)(2pi)/3
View SolutionIf |→c|=2,|→a|=∣∣→b∣∣=1and→a×(→a×→c)+→b=→0 then the acute angle between →aand→c is (A) π6 (B) π4 (C) π3 (D) 2π3
View SolutionIf →a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5and|→c|=7 , then the angle between →aand→b is
View SolutionIf →a,→b,→c are unit vectors such that →a is perpendicular to the plane of →b,→c and the angle between →b,→c is π3, then ∣∣→a+→b+→c∣∣=
View SolutionIf the angles between the vectors →a and →b,→b and →c,→c an →a are respectively π6,π4 and π3, then the angle the vector →a makes with the plane containing →band →c, is
View SolutionIf the angles between the vectors →a and →b,→band→c,→c and →a be π4,π3,π3 respectively, then the angle which →a makes with the plane containing →band→c is
View SolutionIf →a,→b,→c are unit vectors such that →a is perpendicular to the plane of →b,→c and the angle between →b,→c is π3, then ∣∣→a+→b+→c∣∣=
View SolutionIf →a+→b+→c = →0,|→a| = 3 , ∣∣→b∣∣ = 5 and |→c| = 7, find the angle between →a and →b.
View SolutionIf →a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5and|→c|=7 , then the angle between →aand→b is
View SolutionIf →a+→b+→c=0,|→a|=3,∣∣→b∣∣=5and|→c|=7, then the angle between →aand→b is : a)π3 b)π2 c)cos−1(2225) d)π4
View SolutionIf →a,→b,→c are unit vectors such that veca is perpendicular to →band→cand∣∣→a+→b+→c∣∣=1 then the angle between →band→c is (A) π2(B)pi(C)0(D)(2pi)/3
View SolutionIf |→c|=2,|→a|=∣∣→b∣∣=1and→a×(→a×→c)+→b=→0 then the acute angle between →aand→c is (A) π6 (B) π4 (C) π3 (D) 2π3
View Solution
