Statement I: a=ˆi+pˆj+2ˆkandb=2ˆi+3ˆj+qˆk are parallel vectors, iff p=32andq=4.
Statement II: a=a1ˆi+a2ˆj+a3ˆkandb=b1ˆi+b2ˆj+b3ˆk are parallel a1b1=a2b2=a3b3.Solution in Punjabi
Both Statement I and Statement II are correct and statement II is the correct explanation of statement I
Both statement I and statement II are correct but statement II is not the correct explanation of statement I
Statement I is correct but statement II is incorrect
Statement II is correct but statement I is incorrect
The correct Answer is:A
12=p3=2q⇒p=32andq=4
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Passage Based Questions)11videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Matching Type Questions)1videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)7videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel. Also, OA:CB=2:1 and OD:AB=1:3.
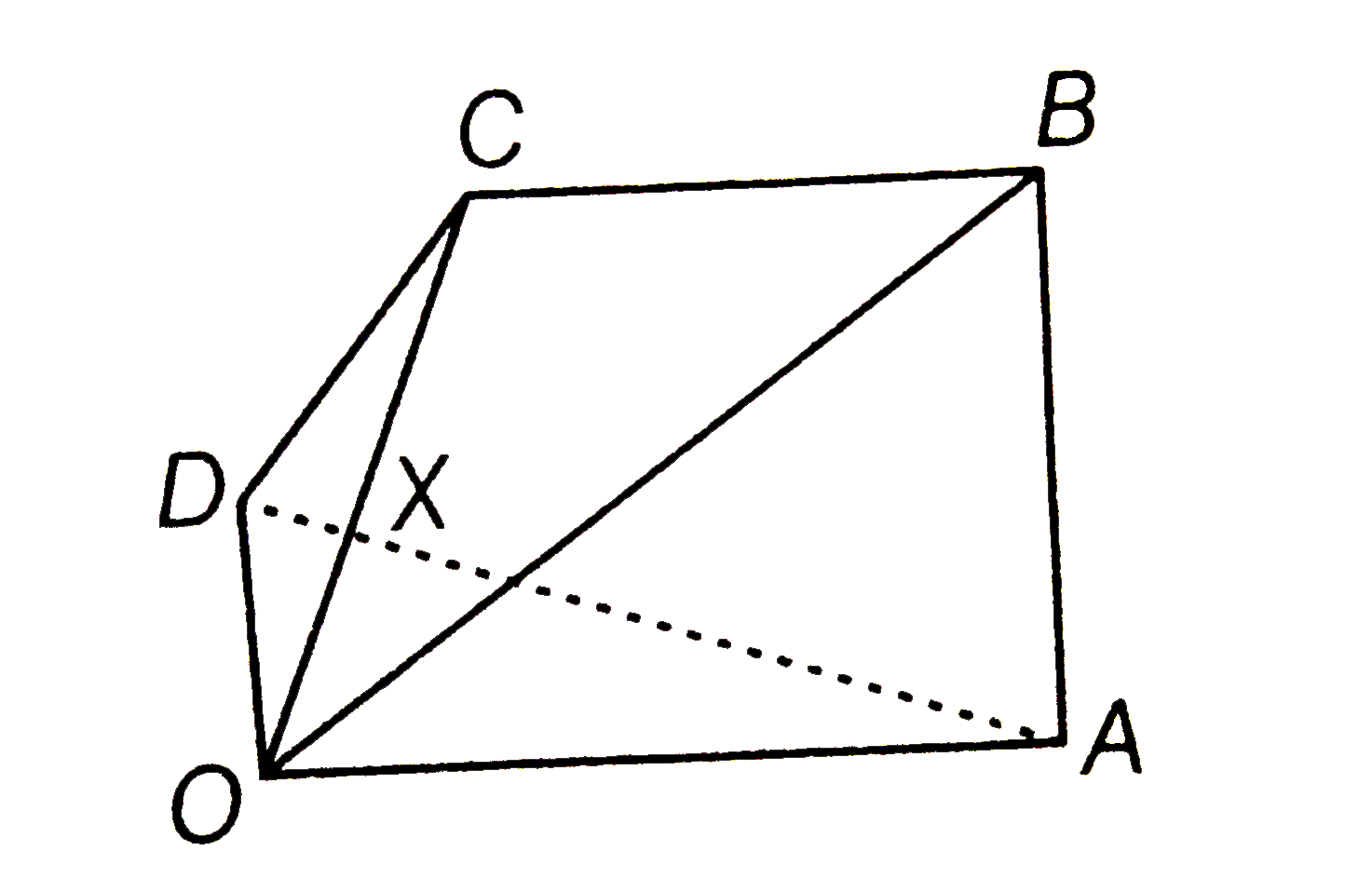
Q. The ratio AXXD is02:15View Solutiona and b form the consecutive sides of a regular hexagon ABCDEF.
 02:47View Solution
02:47View SolutionIf the vectors ˆi−ˆj,ˆj+ˆkand→a form a triangle then →a may be
01:35View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
01:59View Solutiondet[[2a_(1)b_(1),a_(1)b_(2)+a_(2)b_(1),a_(1)b_(3)+a_(3)b_(1)a_(1)b_(2)+a_(2)b_(1),2a_(2)b_(2),a_(2)b_(3)+a_(3)b_(2)a_(1)b_(3)+a_(3)b_(1),a_(3)b_(2)+a_(2)b_(3),2a_(3)b_(3)]]=
01:37View SolutionStatement 1: If a1ˆi+a2ˆj+a3ˆk,→b1ˆi+b2ˆj+b3ˆkandc1ˆi+c2ˆj+c3ˆk are three mutually perpendicular unit vectors then a1ˆi+b1ˆj+c1ˆk,a2ˆi+b2ˆj+c2ˆkanda3ˆi+b3ˆj+c3ˆk may be mutually perpendicular unit vectors.
Statement 2 : value of determinant and its transpose are the same.02:30View SolutionLet →a=a1ˆi+3ˆj+a3ˆk and →b=2ˆi+b2ˆj+ˆk. If →a=→b, find the values of a1,b2 and a3.
02:24View Solutionthe value of the determinant
∣∣ ∣ ∣ ∣ ∣∣(a1−b1)2(a1−b2)2(a1−b3)2(a1−b4)2(a2−b1)2(a2−b2)2(a2−b3)2(a3−b4)2(a3−b1)2(a3−b2)2(a3−b3)2(a3−b4)2(a4−b1)2(a4−b2)2(a4−b3)2(a4−b4)2∣∣ ∣ ∣ ∣ ∣∣ is12:36View Solution→a=a1ˆi+3ˆj+a3ˆk तथा →b=2ˆi+b2ˆj+ˆk यदि →a=→b तब a1,b2 तथा a3 का मान ज्ञात कीजिए।
15:07View Solutionयदि →a=a1ˆi+a2ˆj तथा →b=b1ˆi+b2ˆj शूनयेत्तर सदिश हैं तो साबित करें कि ये समान्तर होंगे यदि और केवल यदि a1b2−a2b1=0.
04:58View Solutionयदि →a=a1ˆi+a2ˆj+a3ˆk तथा →b=b1ˆi+b2ˆj+b3ˆk हो, तो →a×→b का मान कीजिए |
01:53View SolutionLet the vectors →a,→b→c be given as a1ˆi+a2ˆj+a3ˆk,b1ˆi+b2ˆj+b3ˆkc1ˆi+c2ˆj+c3ˆk. Then show that →a×(→b+→c)=→a×→b+→a×→c
04:12View SolutionLet the vectors →a,→b→c be given as a1ˆi+a2ˆj+a3ˆk,b1ˆi+b2ˆj+b3ˆkc1ˆi+c2ˆj+c3ˆk. Then show that →a×(→b+→c)=→a×→b+→a×→c
03:30View SolutionLet the vectors →a,→b→c be given as a1ˆi+a2ˆj+a3ˆk,b1ˆi+b2ˆj+b3ˆkc1ˆi+c2ˆj+c3ˆk. Then show that →a×(→b+→c)=→a×→b+→a×→c
08:37View Solutionमाना a=a1ˆi+a2ˆj+a3ˆk,b=b1ˆi+b2ˆj+b3ˆk
c=c1ˆi+c2ˆj+c3ˆk, यदि |c|=1 तथा (a×b)×c=0, तब ∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣ बराबर है04:12View Solutionकथन-1 : यदि a1ˆi+a2ˆj+a3ˆk,b1ˆi+b2ˆj+b3ˆk तथा c1ˆi+c2ˆj+c3ˆk तीन परस्पर लम्बवत इकाई सदिश हो, तो a1ˆi+b1ˆj+c1ˆk,a2ˆi+b2ˆj+c2ˆk तथा a3ˆi+b3ˆj+c3ˆk परस्पर लम्बवत इकाई सदिश हो सकते है |
कथन-2 : सारणिक तथा इसके प्रतिलोम का मान समान होगा03:29View Solution

