The coordinates of three points O, A, B are (0, 0), (0,4) and (6, 0) respectively. A point P moves so that the area of ΔPOA is always twice the area of ΔPOB. Find the equation to both parts of the locus of P. Solution in Punjabi
The correct Answer is:x2−9y2=0
Step by step video & image solution for The coordinates of three points O, A, B are (0, 0), (0,4) and (6, 0) respectively. A point P moves so that the area of Delta POA is always twice the area of Delta POB. Find the equation to both parts of the locus of P. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Single Option Correct Type Questions)
15 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (More Than One Correct Option Type Questions)
7 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 3
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
37 Videos
Similar Questions
Vertices of a variable triangle are (3,4),(5cosθ,5sinθ) and (5sinθ,−5cosθ), where θ∈R. Locus of its orthocentre is
View SolutionIf (−6,−4),(3,5),(−2,1) are the vertices of a parallelogram, then the remaining vertex can be (0,−1) (b) 7,9) (−1,0) (d) (−11,−8)
View SolutionThe coordinates of the middle points of the sides of a triangle are (4, 2), (3, 3) and (2, 2), then coordinates of centroid are
View SolutionFor every pair of continuous function f,g:[0,1]→R such that max {f(x):x∈[0,1]}=max{g(x):x∈[0,1]}. The correct statement(s) is (are)
View SolutionThe total number of distinct x ∈ R for which
∣∣ ∣ ∣∣xx21+x32x4x21+8x33x9x21+27x3∣∣ ∣ ∣∣=10 is
View SolutionA(5,3),B(3,−2) are two fixed points; find the equation to the locus of a point P which moves so that the area of the triangle PAB is 9 units.
View SolutionLet 0≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be
View SolutionPoint O has coordinates (0, 0), point P lies on the graph of y=6−x2, and point B has coordinates (2√3,0). If OP=BP, the area of triangle OPB is
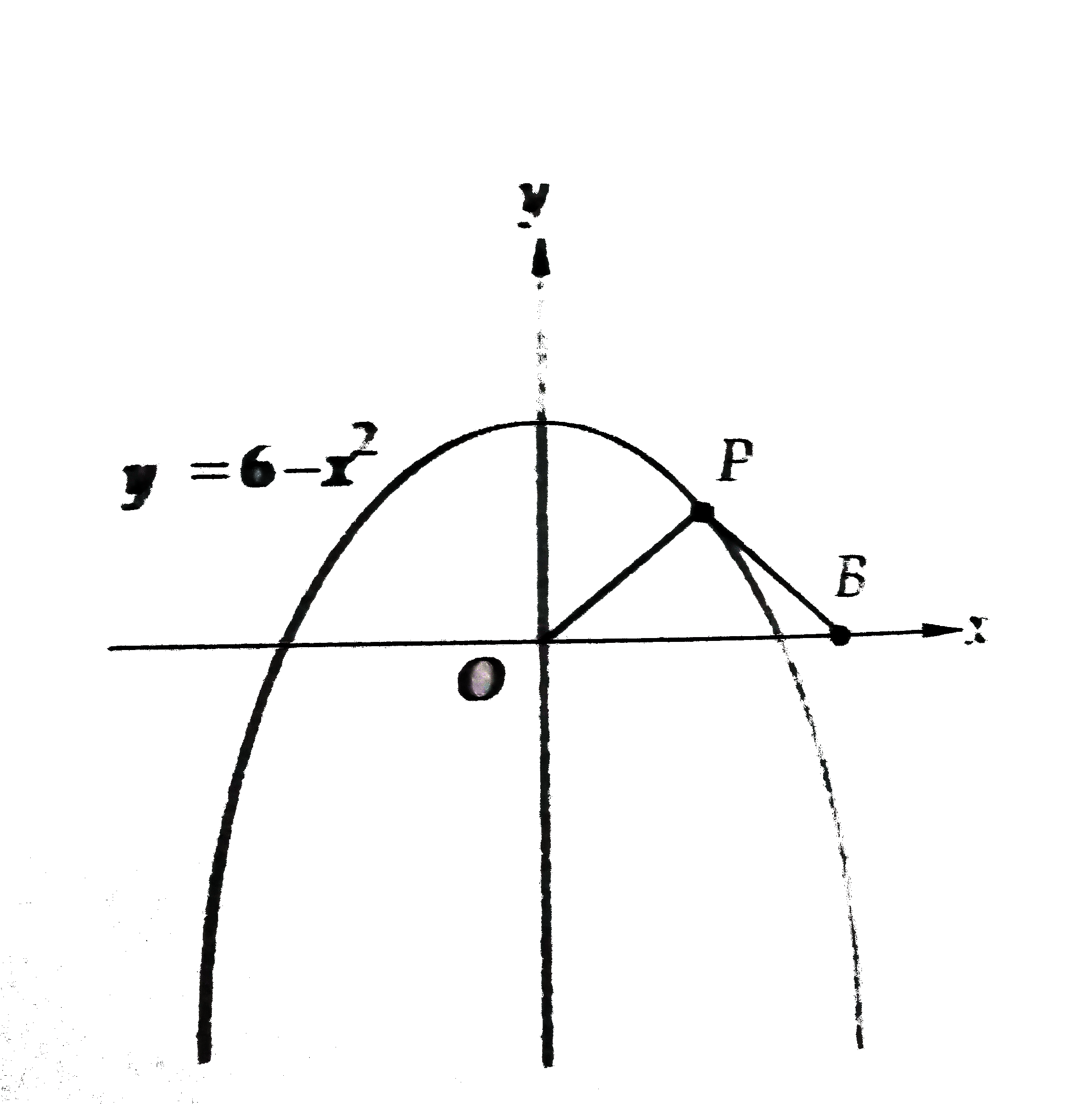
View SolutionO(0,0),A(6,0),B(0,4) are three points. If P is a point such that the area of the quadrilateral PABC is 10 sq. Unit, then the locus of P is
View SolutionGiven A(6,0) and B(0,4) and O is the origin.If the locus P such that area of ΔPOB=2 (area of ΔPOA ) is x2−ky2=0 ,then k is equal to
View SolutionGiven A(6,0) and B(0,4) and 0 is the origin. If the locus P such that area of △POB=2 (area of ΔPOA) is x2−ky2=0 ,then k is equal to
View SolutionO(0.0),A(6,0),B(0,4) are three points.P is a point such that area of ΔPOB is twice the area of ΔPOA ,if locus of P is x2=my2 .then m is equal to
View SolutionLet O be the origin and A, B be the two points having coordinates (0, 4) and (6, 0) respectively. If a point P moves in such a way that the area of the ΔOPA is always twice the area of ΔPOB, then P lies on
View SolutionThe coordinates of the points O, A and B are (0,0), (0,4) and (6,0) respectively. If a point P moves in such a way that trianglePOA Area of always trianglePOB Is twice the area of, then the equation of both parts of the point P of the point P is
View SolutionThe coordinates of the point AandB are (a,0) and (−a,0), respectively. If a point P moves so that PA2−PB2=2k2, when k is constant, then find the equation to the locus of the point P.
View SolutionLet O≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be
View Solution
