A quadrilateral is inscribed in a parabola. Then
a.
the quadrilateral may be cyclic
b.
diagonals of the quadrilateral may be equa
c.l
allpossible pairs of adjacent side may be perpendicular
d. none of theseSolution in Punjabi
the quadrilateral may be cyclic
diagonals of the quadrilateral may be equal
all possible pairs of adjacent sides may be perpendicular
None of the above
The correct Answer is:A, B
Step by step video & image solution for A quadrilateral is inscribed in a parabola. Thena. the quadrilateral may be cyclicb. diagonals of the quadrilateral may be equac.l allpossible pairs of adjacent side may be perpendicular d. none of these by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PARABOLABOOK - ARIHANT MATHSCHAPTER - PARABOLAEXERCISE - Exercise (Passage Based Questions)
23 Videos
- PARABOLABOOK - ARIHANT MATHSCHAPTER - PARABOLAEXERCISE - Exercise (Single Integer Answer Type Questions)
10 Videos
- PARABOLABOOK - ARIHANT MATHSCHAPTER - PARABOLAEXERCISE - Exercise (Single Option Correct Type Questions)
30 Videos
- PAIR OF STRAIGHT LINES BOOK - ARIHANT MATHSCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHSCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
28 Videos
Similar Questions
Consider a parabola P touches coordinate axes at (4,0) and (0,3).
if focus of parabola P is (a,b) then the value of b-a is
View SolutionTwo tangent are drawn from the point (−2,−1) to parabola y2=4x. if α is the angle between these tangents, then find the value of tanα.
View SolutionA common tangent is drawn to the circle x2+y2=a2 and the parabola y2=4bx. If the angle which his tangent makes with the axis of x is π4 , then the relationship between a and b (a,b>0)
View SolutionIf the pair of lines ax2+2(a+b)xy+by2=0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then
View SolutionThere is a rectangular sheet of dimension (2m−1)×(2n−1), (where m>0,n>0) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View SolutionA quadrilateral is inscribed in a parabola. Then (a)the quadrilateral may be cyclic (b)diagonals of the quadrilateral may be equal (c)allpossible pairs of the adjacent side may be perpendicular (d)none of these
View SolutionThe value of |[a,a+d,a+2d] , [a+d,a+2d,a+3d] , [a+2d,a+3d,a+4d]|+|[b
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
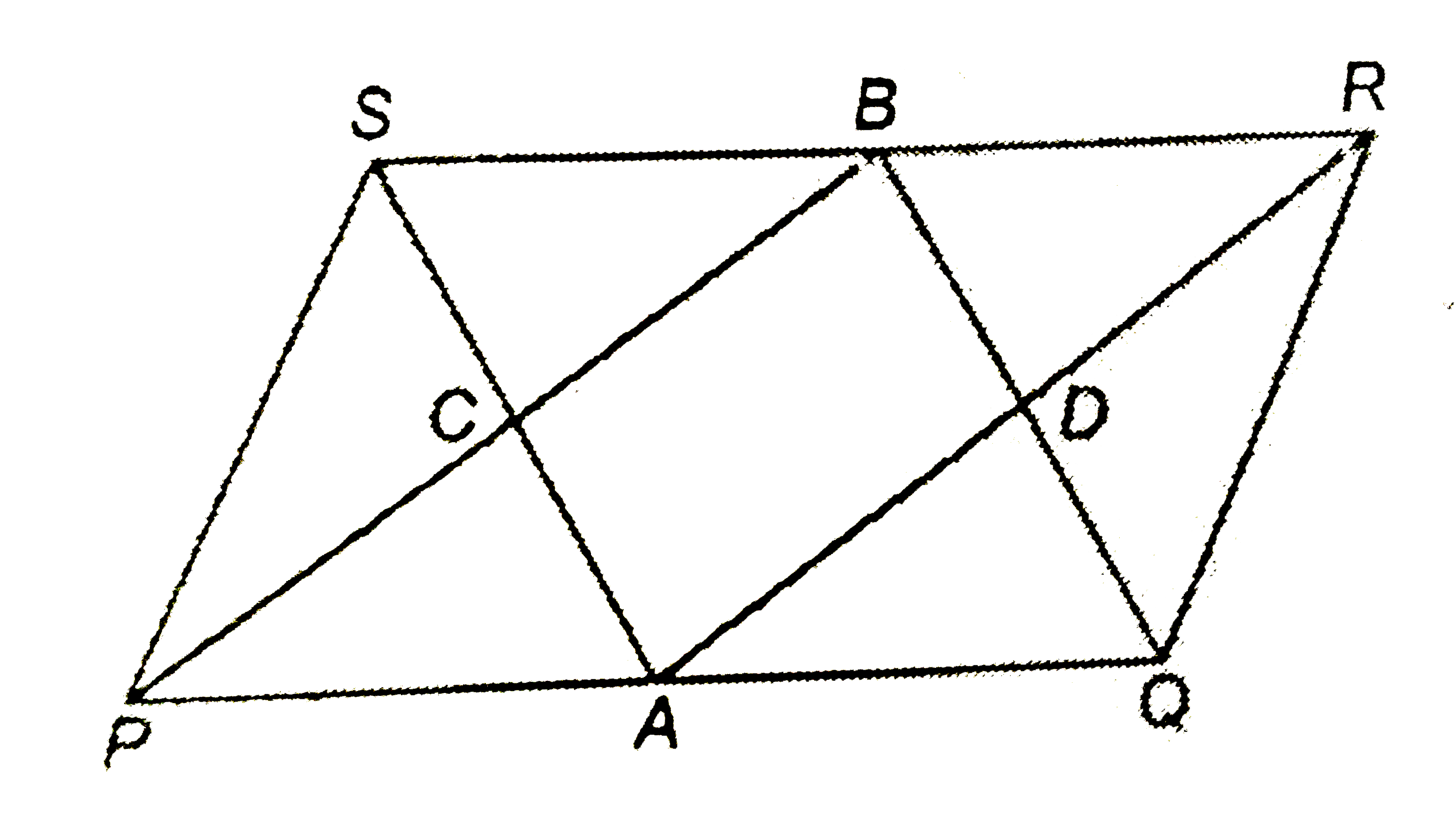
View SolutionIf the diagonals of a cyclic quadrilateral intersect at the centre of a circle , then the quadrilateral is _______________.
View SolutionIf the sides of a cyclic quadrilateral are 3,3,4,4, show that a circle be inscribed in it.
View Solutionएक चतुर्भुज के विकर्ण बराबर तथा परस्पर लम्ब हैं, तो वह चतुर्भुज होगा :
View SolutionIf the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is:
View SolutionA quadrilateral is inscribed in a parabola. Then (a)the quadrilateral may be cyclic (b)diagonals of the quadrilateral may be equal (c)allpossible pairs of the adjacent side may be perpendicular (d)none of these
View SolutionThe diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View Solutionसमानान्तर चतुर्भुज PQRS में, A एवं Bकी स्थिति इस प्रकार है कि वे विकर्ण QS के दोनों ओर क्रमशः P एवं R से रेखांकित लम्ब का आधार बनाते हैं। AP एवं BR किस प्रकार सम्बन्धित हैं?
View SolutionWhich of the following statements is/are correct?
The intersections of the angle bisectors of the quadrilateral are the vertices of the cyclic quadrilateral
If diagonals of a cyclic quadrilateral perpendicularly intersect at point P, then the line through P, perpendicular to any side bisects the opposite side.
The product of the lengths of the two diagonals of a cyclic quadrilateral is equal to the sum of the products of opposite sides.
View Solution
