Solve limx→0[sinxx]
(where [.] denotes greatest integer function)Solution in Punjabi
The correct Answer is:[ as x→0−h⇒t→1−h∴[t]=0]
Step by step video & image solution for Solve lim_(xto0)[(sinx)/x] (where [.] denotes greatest integer function) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - SOLVED EXAMPLES
1 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Single Option Correct Type Questions)
38 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
Similar Questions
To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
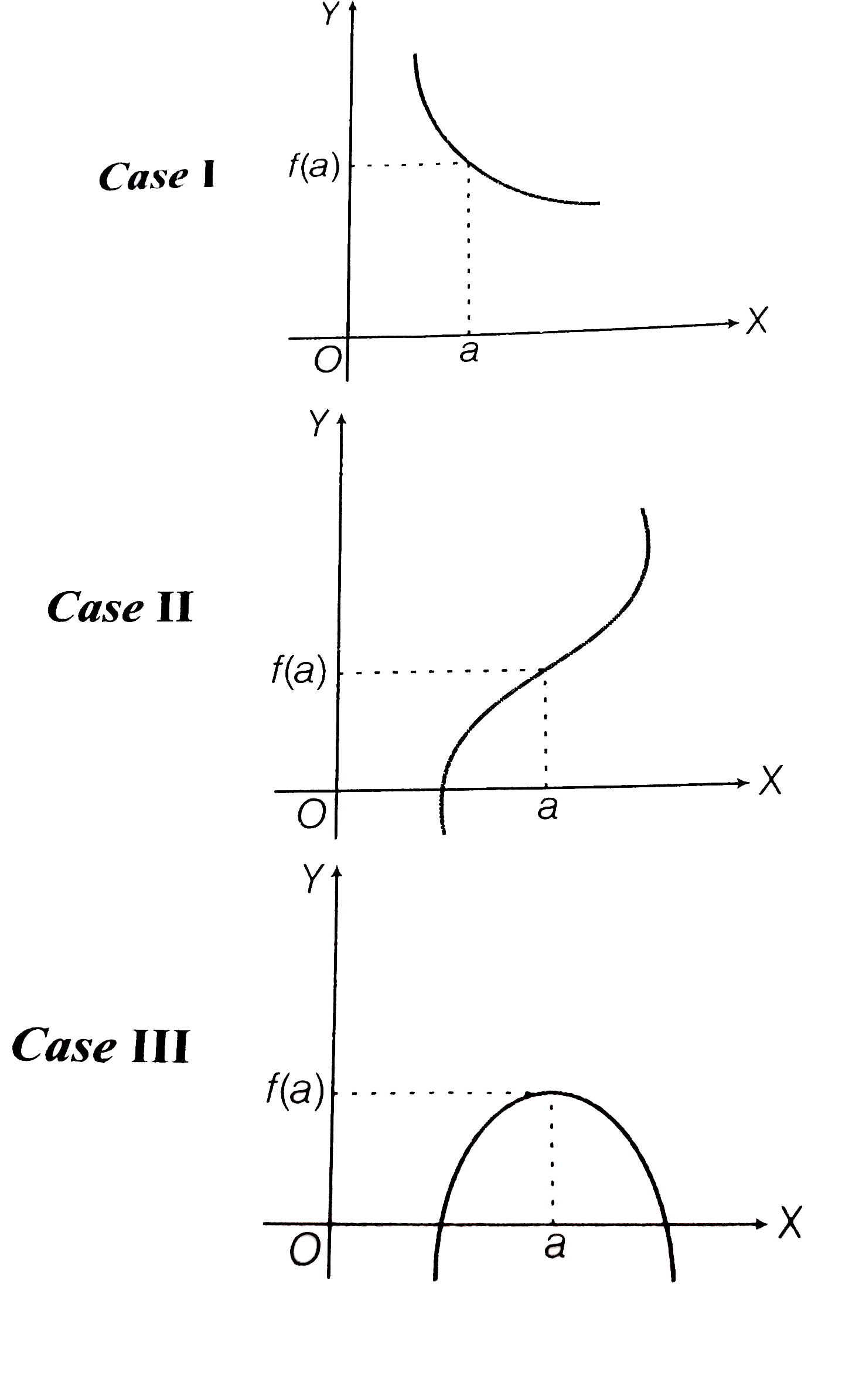
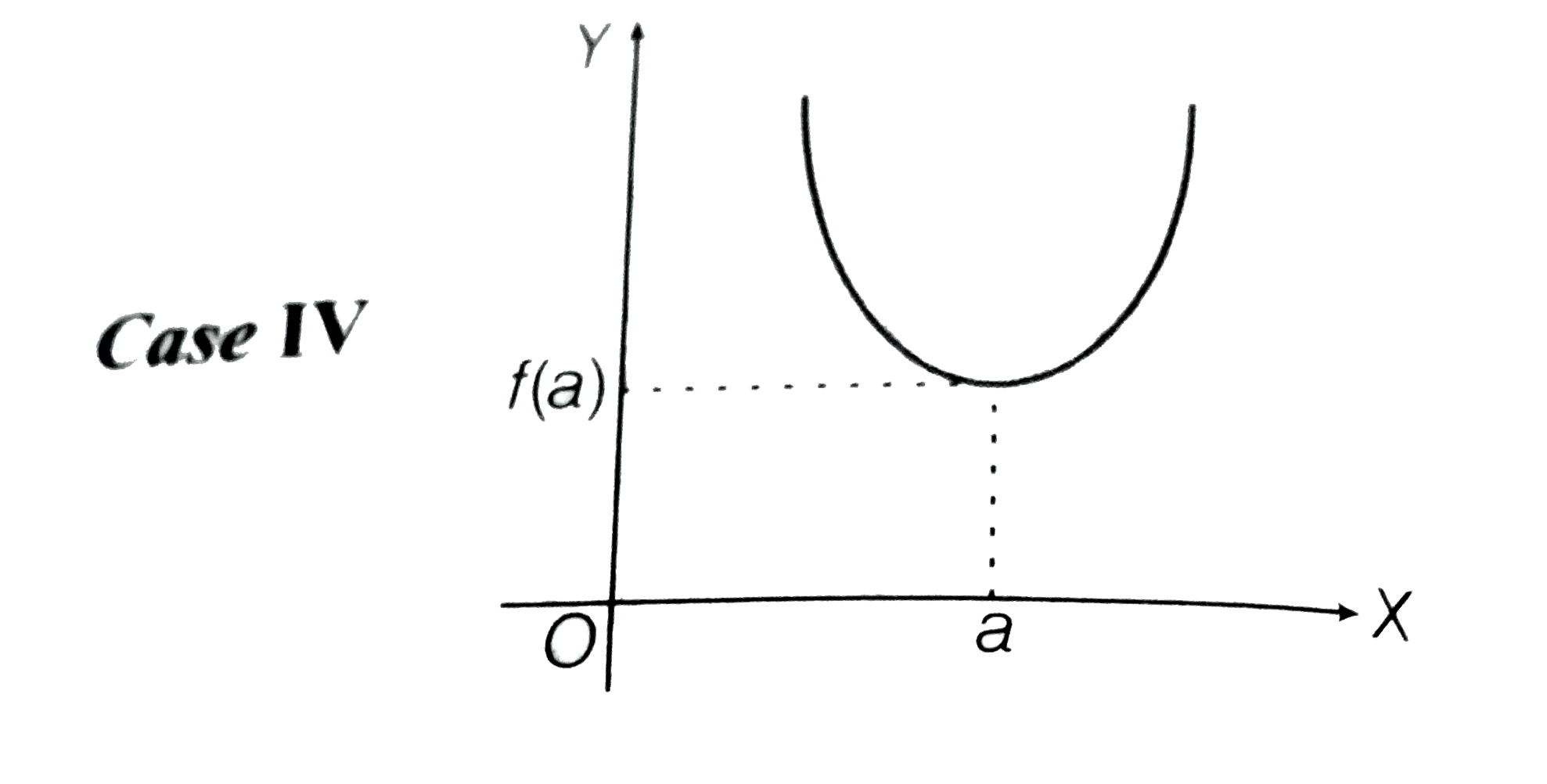
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=−3 and limx→1[f(x)−12] does not exist, (where [.] denotes the greatest integer function), then
View Solutionlimx→0sin(πcos2(tan(sinx)))x2 is equal to
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionIn Which quadrant Point (−2,−3) will be lie.
View SolutionSolve (i) limx→1sinx (ii) limx→0+[sinxx]
(iii) limx→0−[sinxx]
(where [.] denotes greatest integer function)
View SolutionSolve (i) limx→0+[tanxx]
(ii) limx→0−[tanxx]
(where [.] denotes greatest integer function)
View SolutionSolve limx→0[sin|x|x], where e[.] denotes greatest integer function.
View SolutionSolve limx→0[sin|x||x|], where [.] denotes greatest integer function.
View Solutionlimx→0[−2xtanx], where [.] denotes greatest integer function is
View Solutionlimx→0[msinxx] is equal to (where mεI and [.] denotes greatest integer function)
View Solutionlimx→0[min(y2−4y+11)sinxx] (where [.] denotes the greatest integer function) is
View SolutionSolve (i) limx→1sinx (ii) limx→0+[sinxx]
(iii) limx→0−[sinxx]
(where [.] denotes greatest integer function)
View SolutionSolve (i) limx→0+[tanxx]
(ii) limx→0−[tanxx]
(where [.] denotes greatest integer function)
View SolutionSolve limx→0[sin|x|x], where e[.] denotes greatest integer function.
View Solutionlimx→0[−2xtanx], where [.] denotes greatest integer function is
View Solution
