Let S be the sum of all possible determinants of order 2 having 0,1,2 and 3 as their elements,. Find the common root α of the equations x2+ax+[m+1]=0,
x2+bx+[m+4]=0
and x2−cx+[m+15]=0
such that α>Swherea+b+c=0 and
m=limn→001n2n∑r=1r√n2+r2
and [.] denotes the greates integer function. Solution in Punjabi
The correct Answer is:=√5−1
Step by step video solution for Let S be the sum of all possible determinants of order 2 having 0,1,2 and 3 as their elements,. Find the common root alpha of the equations x^(2)+ax+[m+1]=0, x^(2)+bx+[m+4]=0 and x^(2)-cx+[m+15]=0 such that alphagtSwherea+b+c=0 and m=lim_(n to 00)(1)/(n)sum_(r=1)^(2n)(r)/(sqrt(n^(2)+r^(2))) and [.] denotes the greates integer function. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBook:ARIHANT MATHSChapter:LIMITSExercise:SOLVED EXAMPLES
Explore 1 Video
- LIMITSBook:ARIHANT MATHSChapter:LIMITSExercise:Exercise (Single Option Correct Type Questions)
Explore 38 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:ARIHANT MATHSChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 8 Videos
- LOGARITHM AND THEIR PROPERTIESBook:ARIHANT MATHSChapter:LOGARITHM AND THEIR PROPERTIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 4 Videos
Similar Questions
To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
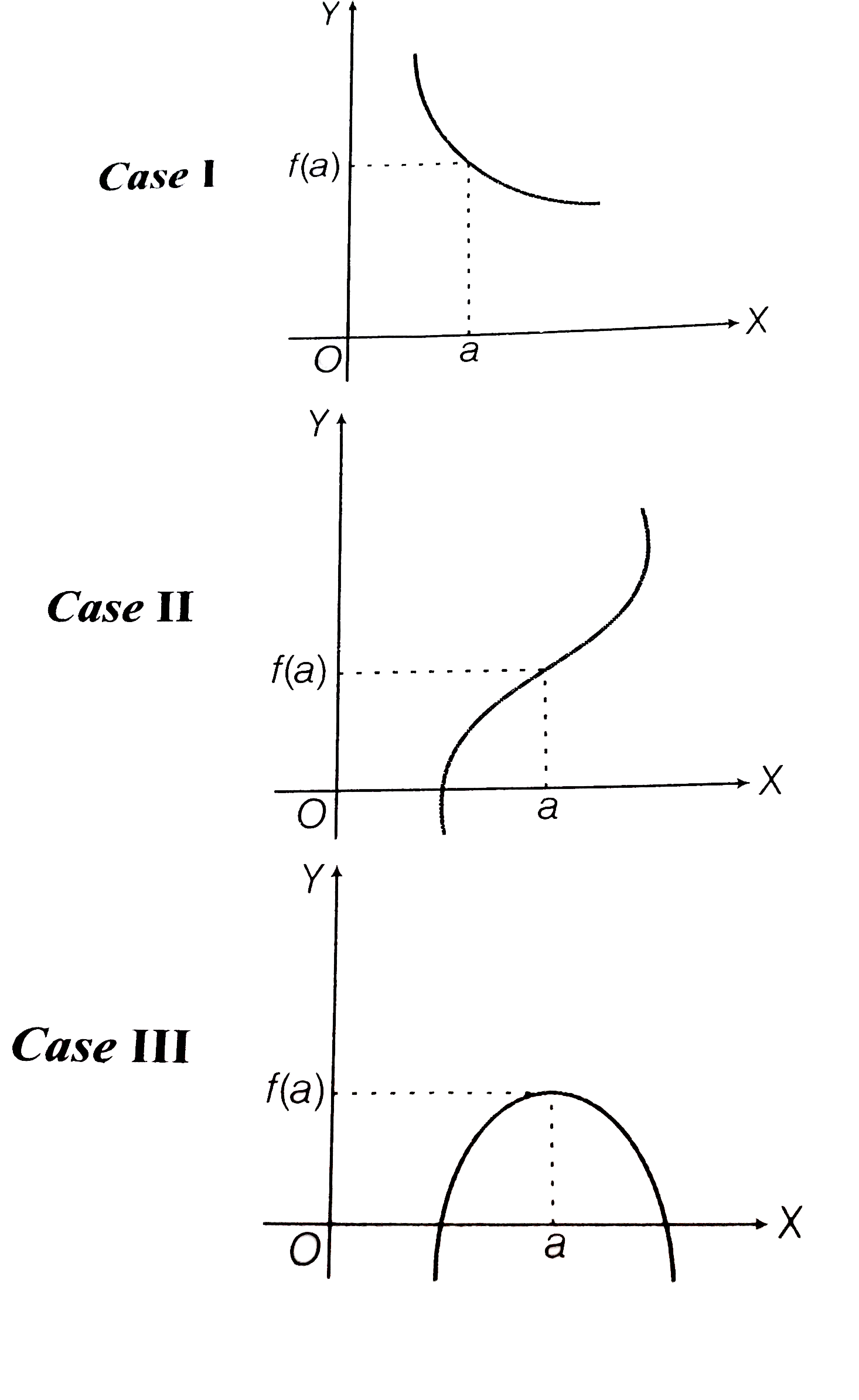

Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=−3 and limx→1[f(x)−12] does not exist, (where [.] denotes the greatest integer function), then
View Solutionlimx→0sin(πcos2(tan(sinx)))x2 is equal to
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionIn Which quadrant Point (−2,−3) will be lie.
View SolutionIf sum_(r=0)^(2n)a_(r)(x-100)^(r)=sum_(r=0)^(2n)br(x-101)^(r) and a_(k)=(2^(k))/(kC_(n))AA k>=n then b_(-) n equals ( A )2^(n)(2^(n+1)-1)(B)2^(n)(2^(n)-1)(C)2^(n)(2^(n)+1)(D)2^(n+1)(2^(n)-1)
View SolutionLet t_(r) denote the r^(th) term of an A.P.Also suppose t_(m)=(1)/(n) and t_(n)=(1)/(m) for some positive integers m and n then which of the following is necessarily a root of the equation? (l+m-2n)x^(2)+(m+n-2l)x+(n+l-2m)=0
View SolutionIf [x] denotes the integral part of x and m=[|x|1+x2],n= integral values of 12−sin3x then (A) m≠n (B) m>n (C) m+n=0 (D) nm=0
View Solutionn∑r=1(ar+br),a,b∈R+ is equal to :
View SolutionIf (1+x)n=C0+C1x+C2x2+…and+Cnxn
Σ50r=0C2r(r+1)=m!(n!)2, then the value of (m+n) is equal to (where Cr represents .nCr )
View Solutionn∑r=0(−1)r nCr(12r+3r22r+7r23r+15r24r+....+m पद) श्रेणी का योगफल है
View Solutionn∑r=0(−1)r^nCr[12r+322r+723r+1524r+up→mterms]=2mn−12mn(2n−1)
View SolutionWite down the corresponding elements in the figure : 1)……………… br 2)…………… br 3).……………. Br 4)………….. Br 5)…………. Br 6)…………..
View SolutionLet S be the sum of all possible determinants of order 2 having 0,1,2 and 3 as their elements,. Find the common root α of the equations x2+ax+[m+1]=0,
x2+bx+[m+4]=0
and x2−cx+[m+15]=0
such that α>Swherea+b+c=0 and
m=∑n→001n2n∑r=1r√n2+r2
and [.] denotes the greates integer function.
View Solutionn∑r=1(ar+br),a,b∈R+ is equal to :
View SolutionIf [x] denotes the integral part of x and m=[|x|1+x2],n= integral values of 12−sin3x then (A) m≠n (B) m>n (C) m+n=0 (D) nm=0
View SolutionIf m=∞∑r=0arn=∞∑r=0br,where0,a<1,0,b<1 then the quandratic equation whose roots are a and b is (A) mnx2+(m+n−2mn)x=mn−m−n+1=0 (B) mnx2+(2mn−m−n)x=mn−m−n+1=0 (C) mnx2+(2mn+m+n)x=mn+m+n+1=0 (D) mnx2+(2mn+m+n)x=mn+m+n+1=0
View Solution