Let xtanα+ysinα=α and xαcosecα+ycosα=1 be two variable straight lines, α being the parameter. Let P be the point of intersection of the lines. In the limiting position when a→0, the point P lies on the line :Solution in Punjabi
(2,−1)
(2,1)
(−2,1)
(−2,−1)
The correct Answer is:A, B, D
Step by step video & image solution for Let xtan alpha + ysin alpha= alpha and xalpha cosec alpha + ycosalpha= 1 be two variable straight lines, alpha being the parameter. Let P be the point of intersection of the lines. In the limiting position when a ->0, the point P lies on the line : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Passage Based Questions)
10 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - SOLVED EXAMPLES
1 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
Similar Questions
If limx→∞4x(π4−tan−1(x+1x+2))=y2+4y+5 then y can be equal to
View SolutionIf limx→af(x)=1 and limx→ag(x)=∞ then limx→a{f(x)}g(x)=elimx→a(f(x)−1)g(x)
limx→0(sinxx)sinxx−sinx is equal to
View SolutionTo evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
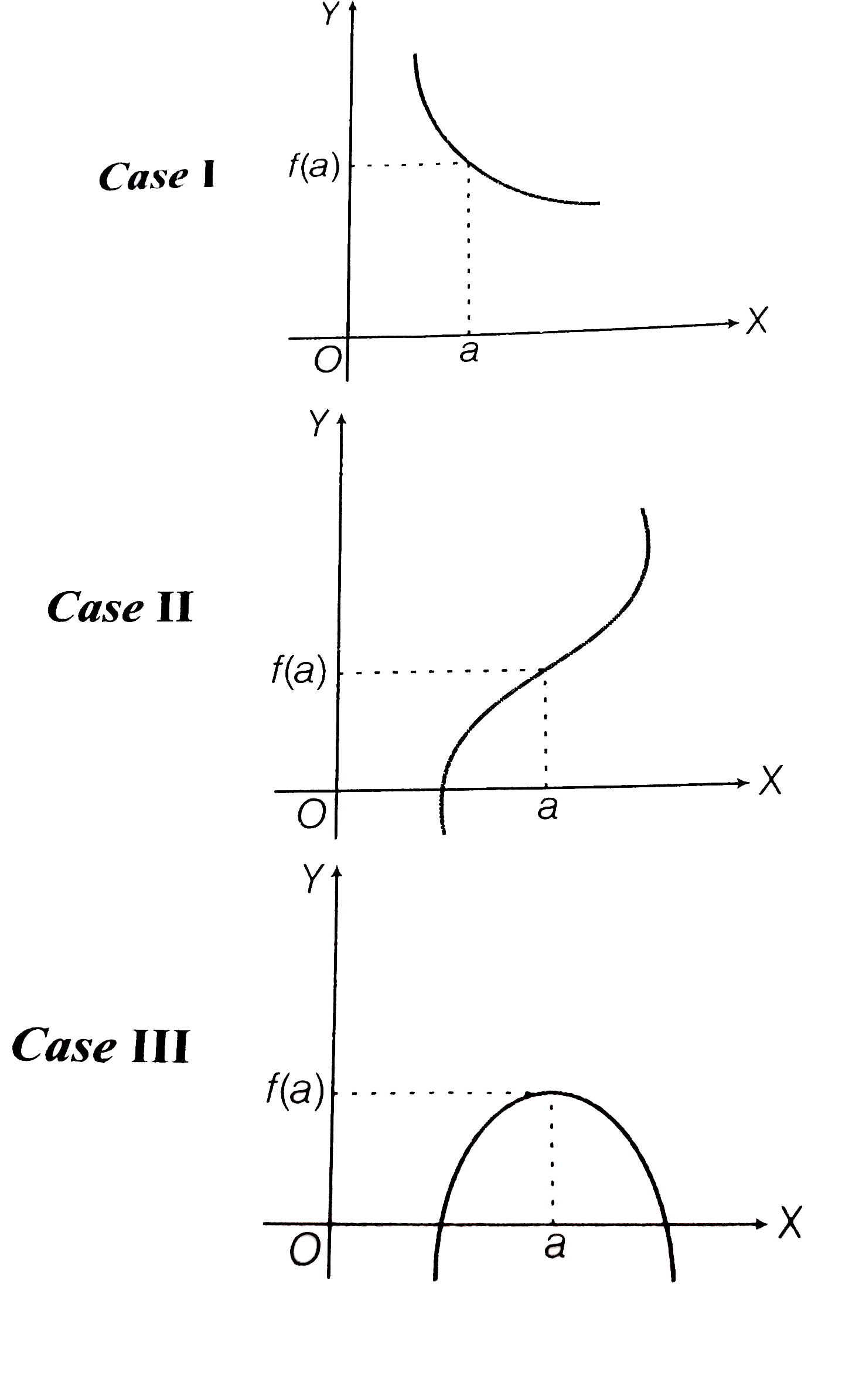
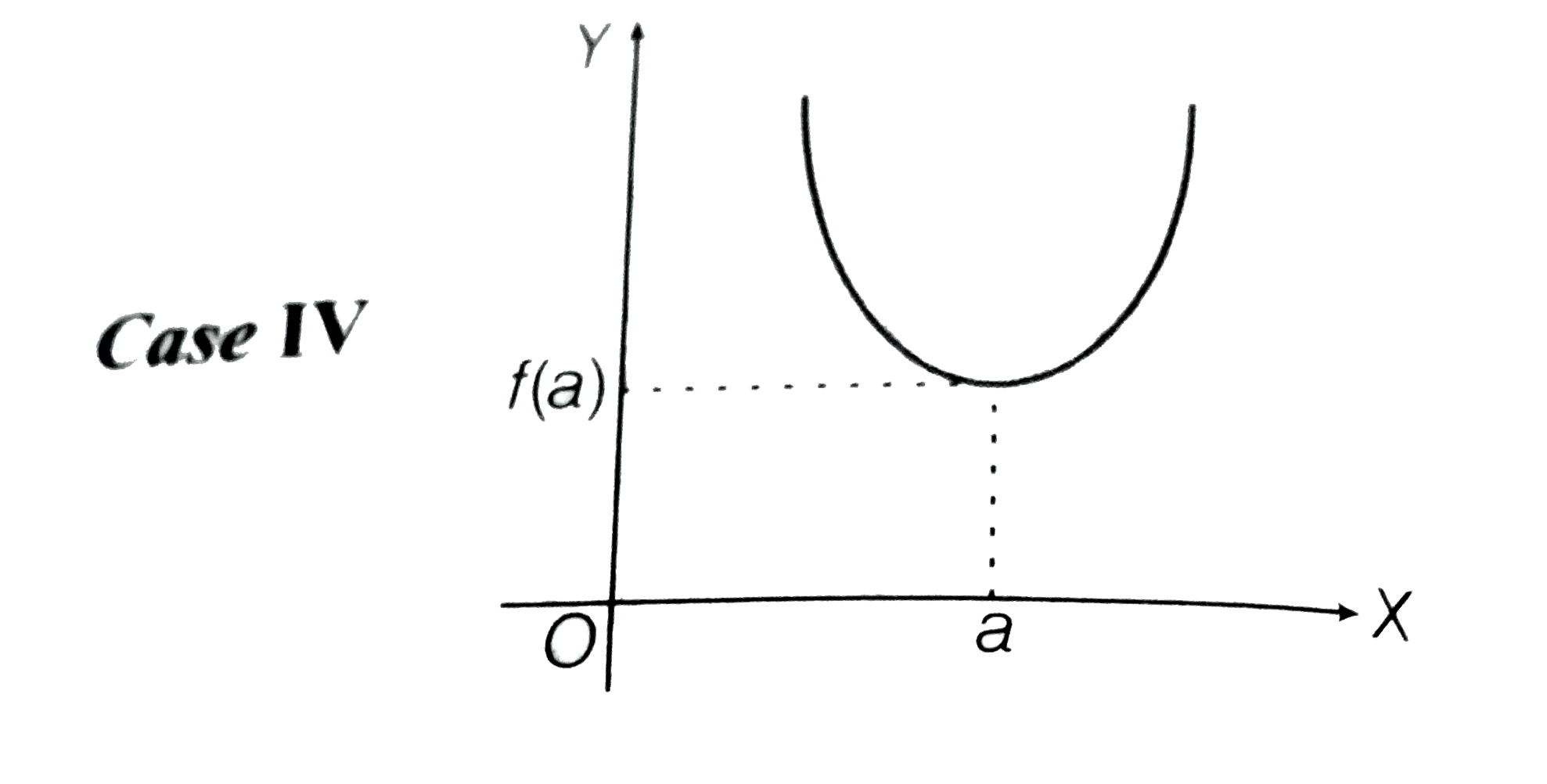
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=−3 and limx→1[f(x)−12] does not exist, (where [.] denotes the greatest integer function), then
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionIn Which quadrant Point (−2,−3) will be lie.
View SolutionLet tan alpha . x + sin alpha · y = alpha and alpha. cosec alpha • x + cosalpha · y = 1 be two variable straight lines, alpha being the parameter. Let P be the point of intersection of the lines. In the limiting position when a ->0, the point P lies on the line :
View Solutionमाना रेखा l:xcosα+ysinα=P है पर अक्षों द्वारा
रेखा l पर अक्षों द्वारा काटे गए अंतः खण्डों का मान होगा
View Solutionमाना रेखा l:xcosα+ysinα=P है पर अक्षों द्वारा
रेखा l पर अक्षों द्वारा काटे गए अंतः खण्डों का मध्य बिंदु का बिंदुपथ होगा
View SolutionThe locus of the point of intersection of the lines xcosα+ysinα=aandxsinα−ycosα=b, where α is a parameter is
View Solutionरेखाओं xcosα+ysinα=p तथा xsinα−ycosα=q (alhpa एक चर है) के प्रतिच्छेद बिन्दु का बिन्दुपथ होगा
View SolutionThe locus of the point of intersection of the lines xcosα+ysinα=p and xsinα−ycosα=q, α is a variable will be
View SolutionIf the point (3,4) lies on the locus of the point of intersection of the lines xcosα+ysinα=a and xsinα−ycosα=b (α is a variable) ,the point (a,b) lies on the line 3x−4y=0 then |a+b| is equal to
View Solutionদেখাও যে xcosα+ysinα=p সরলরেখার সমীকরণকে নিচের আকারে দেখা যায়: x−pcosα−sinα=y−psinαcosα=r
View Solutionxcosα+ysinα=p, xcosβ+ysinβ=q এবং y=xtanθ সরলরেখা তিনটি একবিন্দুগামী হওয়ার শর্ত নির্ণয় করো।
View Solutionα একটি পরিবরতনশীল চল হলে দেখাও যে, xcosα+ysinα=α এবং xsinα−ycosα=α সরলরেখার দুটির ছেদবিন্দুর সঞ্চারপথ একটি বৃত্ত।
View SolutionIf the point (3, 4) lies on the locus of the point of intersection of the lines xcosα+ysinα=a and xsinα−ycosα=b (α is a variable), the point (a, b) lies on the line 3x−4y=0 then |a+b| is equal to
View Solution
