Statement I If f(x) is a continuous function defined from R to Q and f(5)=3, then differential coefficient of f(x)w.r.t.x will be 0
Statement II Differentation of constant functions is always zero.Solution in Punjabi
Both statement I and Statement II are correct and Statement II is the correct explanation of Statement I
Both Statement I and Statement II are correct but Statement II is not the correct explanation of Statement I
Statement I is correct but Statement II is incorrect
Statement II is correct but Statement I is incorrect.
The correct Answer is:A
Step by step video & image solution for Statement I If f(x) is a continuous function defined from R to Q and f(5)=3, then differential coefficient of f(x) w.r.t.x will be 0 Statement II Differentation of constant functions is always zero. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIATION EXERCISE - Exercise (Passage Based Questions)
16 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIATION EXERCISE - Differentiation Exercise 5:
2 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIATION EXERCISE - Exercise (More Than One Correct Option Type Questions)
62 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
26 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHSCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
Let f(x+y)−f(x)2=f(y)−12+xy, for all x,y∈R,f(x) is differentiable and f'(0)=1. Domain of log(f(x)), is
View SolutionMatch the entries between the following two columns.

View SolutionIf y=secx−tanxsecx+tanx, then dydx equals.
View SolutionIf f:R−{−1}→Randf is differentiable function satisfies:
f((x)+f(y)+xf(y))=y+f(x)+yf(x)∀x,
y∈R−{_1} Find f(x).
View SolutionThe slope of the tangent to the curve (y−x5)2=x(1+x2)2 at the point (1,3) is.
View Solutionनिम्नलिखित कथनो पर विचार कीजिए
I. मान लीजिए f:R→R वास्तविक फलन इस प्रकार है की |f(x)−f(y)|≤|x−y|3,∀x,y∈R, तब f(x) एक अचर फलन होगा
II. यदि किसी वास्तविक फलन f(x) का x के सापेक्ष अवकल गुणांक शून्य हो, तो फलन अचर होता है
उपरोक्त कथनो में से कौन-सा/से कथन है/है ?
View SolutionStatement I If f(x) is a continuous function defined from R to Q and f(5)=3, then differential coefficient of f(x)w.r.t.x will be 0
Statement II Differentation of constant functions is always zero.
View SolutionThe function f:R→R is defined as f(x)=3−x. From the following statements,
I. f is one-one
II. f is onto
III. f is a decreasing function the true statements are
View SolutionConsider the functions, f(x) = |x -2 | + |x - 5 |, x ∈ R Statement-1 : f'(4) = 0 Statement-2 : f is continuous in [2, 5], differentiable in (2, 5) and F(2) =F(5)
View SolutionConsider the function f(x)=|x−2|+|x−5|,xεR
Statement 1: f'(4)=0
Statement 2: f is continuous in [2,5] differentiable in (2,5) and f(2)=f(5).
View SolutionConsider the function f(x)=|x−2|+|x−5|,x∈R.
Statement-I : f'(4)=0.
Statement-II : f is continuous is [2, 5], differentiable in (2, 5) and f(2)=f(5).
View Solutionवक्तव्य I यदि f(x) सतत है, तब |f(|x|)| भी सतत फलन है।
वक्तव्य II यदि f(x)≥|x|,AaxεR, तब x=0 पर |f(x)| सतत है।
View SolutionLet f be a differentiable function defined on R such that f(0) =−3. If f'(x) ≤5 for all x then
View Solutionकथन-I : माना से Q तक परिभाषित फलन f (x) संतत् है तथा f(5) = 3 तो x के सापेक्ष f (x) का अवकलन गुणांक शून्य होगा।
क्योंकि कथन- II : अचर फलन का अवकलन सदैव शून्य होता है।
View Solutionवक्तव्य । फलन f(x) जो निम्न ग्राफ द्वारा प्रदर्शित है, x = a पर अवकलनीय है।
वक्तव्य ॥ फलन f(x), x = a पर सतत् है।
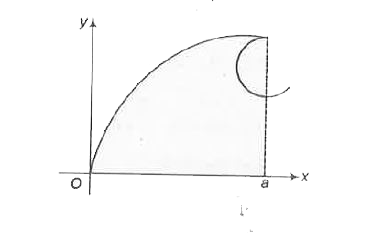
View SolutionIf the function f defined on R-{0} is a differentiable function and f(x3)=x5 for all x,
then f'(27)=
View Solution
