Let f(x){1+x,0≤x≤23−x,2<x≤3:
Find fof.Solution in Punjabi
The correct Answer is:(fof)(x)=⎧⎪⎨⎪⎩2+x,0≤x≤12−x,1<x≤24−x,2<x≤3
Step by step video & image solution for Let f (x) { {:(1+x"," , 0 le x le 2),( 3-x"," ,2 lt x le 3):}:Find fof. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 1
5 Videos
- FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 2
6 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHSCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHSCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
Which of the following graphs are graphs of a function?

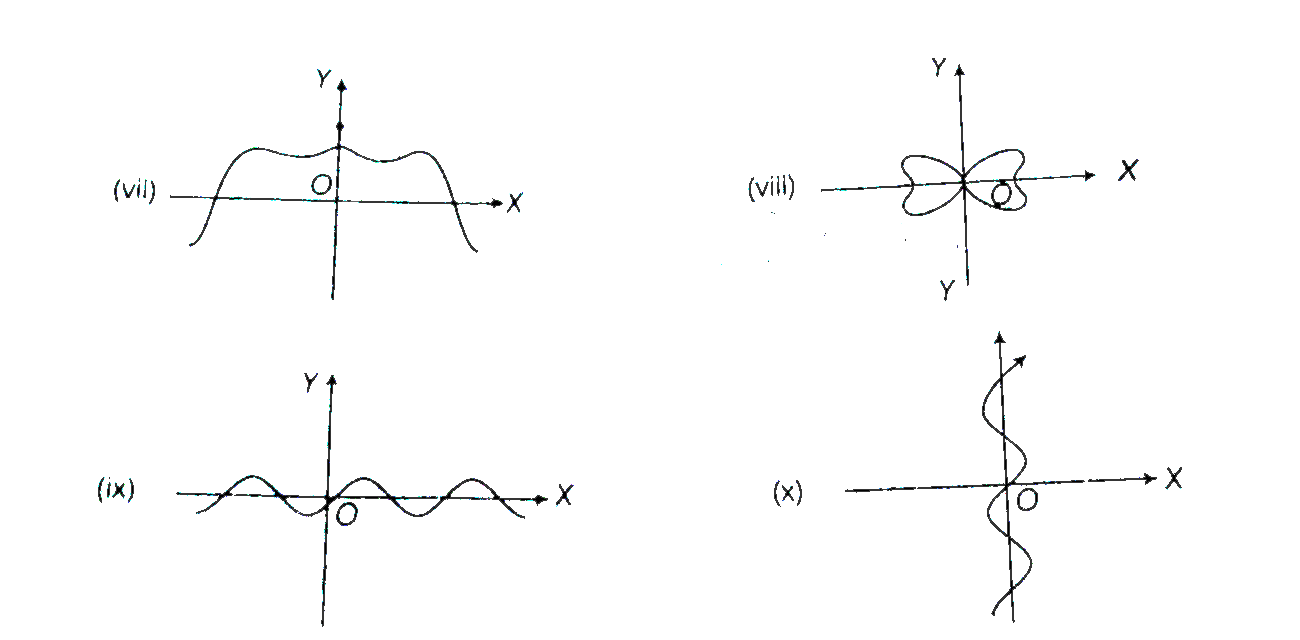
View SolutionThe domain of the function
f(x)=√x2−5x+6+√2x+8−x2 , is
View SolutionThe number of solutions of the equation |x−1|−|2x−5|=2x
View SolutionFind the number of solutions of the equation x21−|x−2|=1, graphically.
View SolutionIf f(x)=⎧⎨⎩x220≤x<12x2−3x+321≤x≤2 then,
View Solutionनिम्नलिखित फलन के अवकलनीयता की विवेचना कीजिए -
f(x)=⎧⎪⎨⎪⎩2x+3,−3<x<−2x+1,−2≤x<0x+2,0≤x≤1
View SolutionLet f(x)=x3−x2+x+1andg(x)={maxf(t),0≤t≤xfor0≤x≤13−x,1<x≤2 Then, g(x) in [0, 2] is
View SolutionLet f(x)=−x3+x2−x+1andg(x)={min(f(t)),0≤t≤xand0≤x≤1x−1,1<x≤2 Then, the value of limx→1g(g(x)), is........ .
View SolutionLet f(x)={1+x,0≤x≤23−x,2<x≤3
find (fof) (x).
View SolutionIf f(x)=⎧⎪⎨⎪⎩3, if 0≤x≤14, if 1<x<35, if 3≤x≤10, then
View SolutionIf f(x)={1+x0≤x≤23x−22<x≤3, then f(f(x)) is not differentiable at:
View SolutionLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x3+x2−10x−1≤x<0cosx0≤x<π21+sinxπ2≤x≤x Then at x=π2, f(x) has:
View Solutionमाना f(x)=x3−x2+x+1 और g(x)={max{f(t),0≤t≤x}0≤x≤13−x1<x≤2
फलन g(x) की सततता तथा अवकलनीयता अंतराल (0, 2) पर ज्ञात कीजिए |
View Solutionf(x)={(x,0,≤,x,≤,2),(3x,−,1,2,<,x,≤,3) then f'(2+) is:
View Solutionf(x)=⎧⎪⎨⎪⎩3,if0≤x≤14,if1<x<35,if3≤x≤10
View SolutionLet f(x)=x3−x2+x+1 g(x) = max I {f(t),0≤t≤x},0≤x≤1=3−x,1<x≤2
Then in [0, 2] the points where g(x) is not differentiable is………
View Solution
