Which one of the following curves represents the solution of the initial value problem dydx=100−y, where y(0)=50Solution in Punjabi
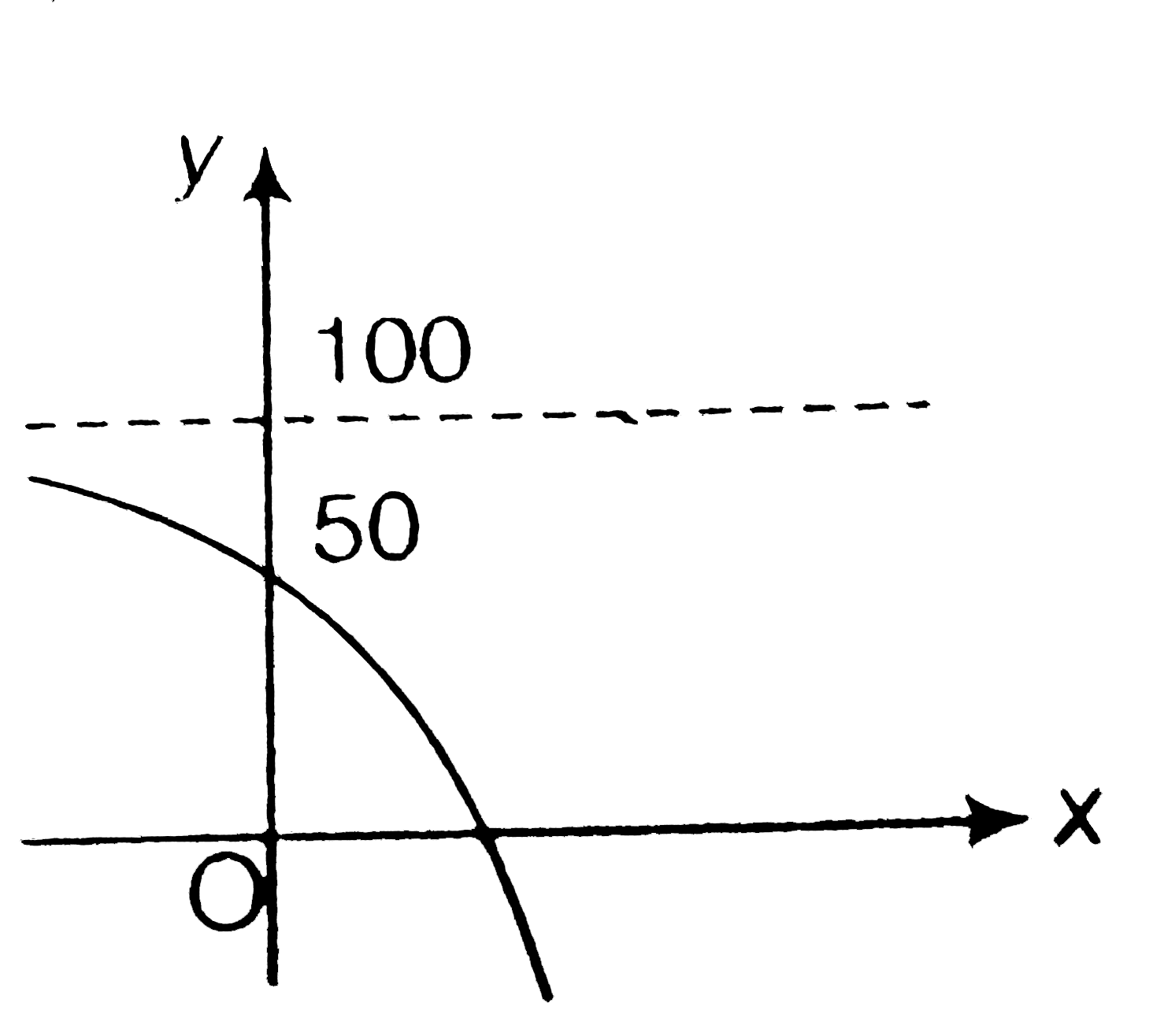

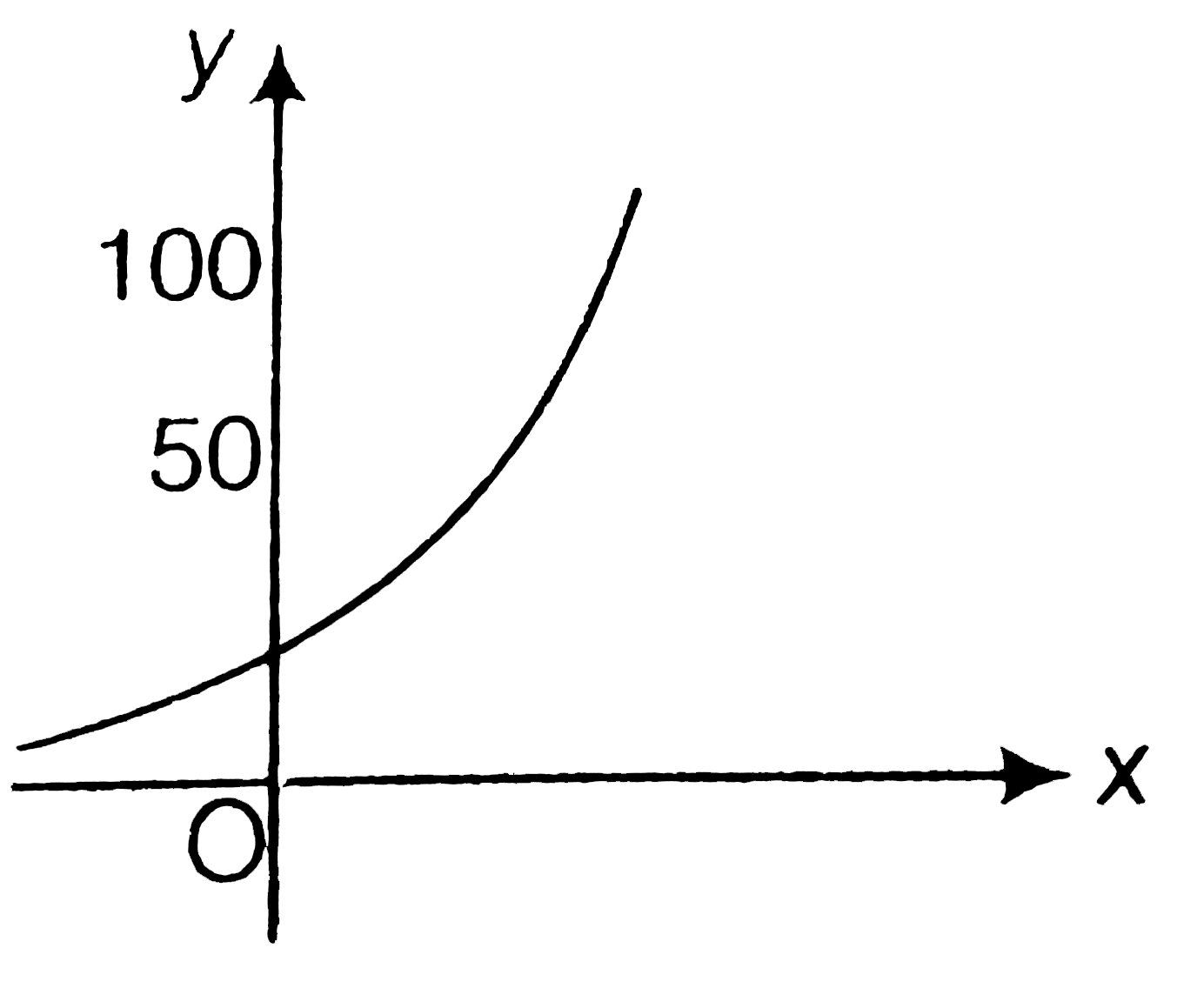
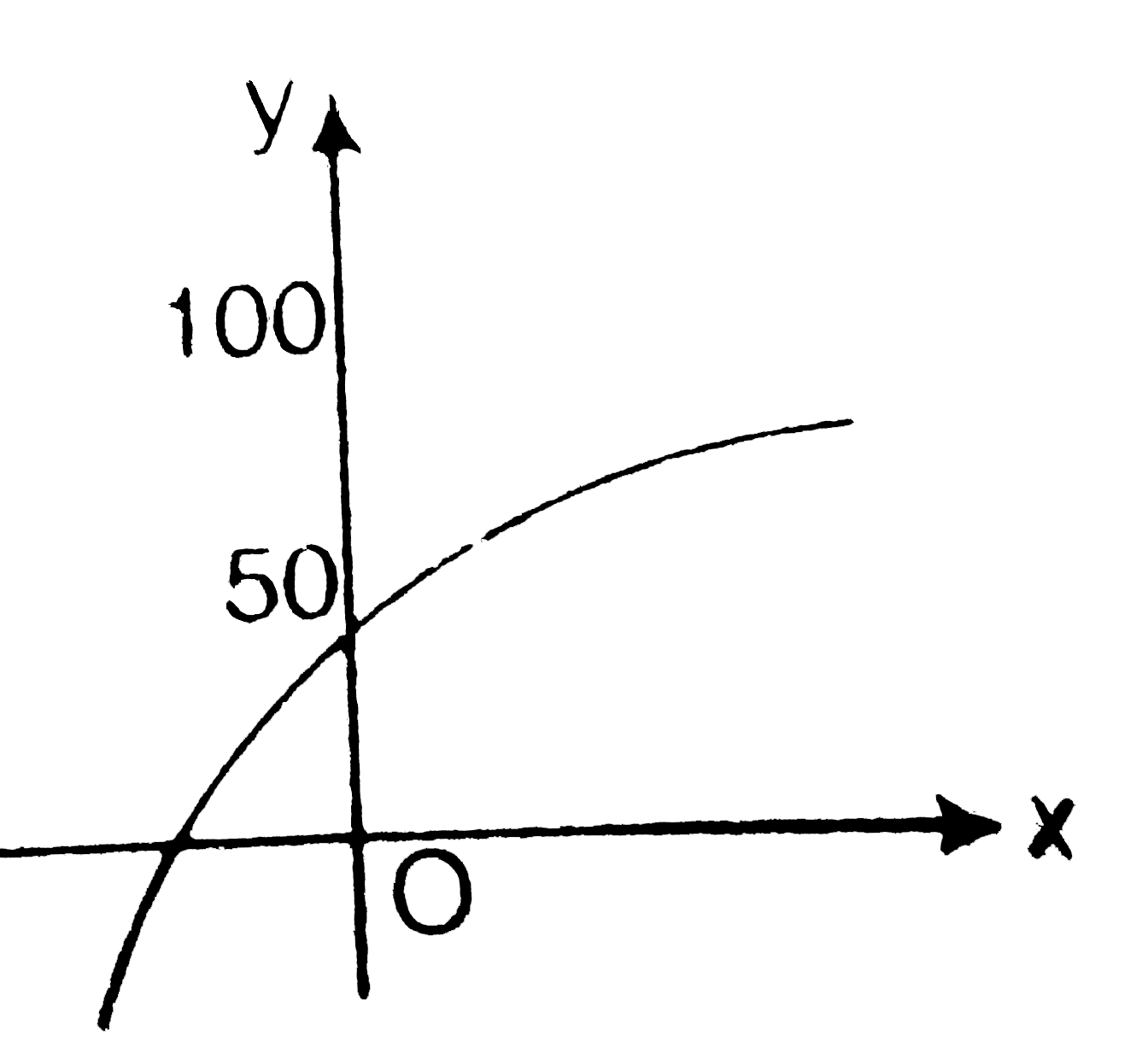
The correct Answer is:B
Step by step video & image solution for Which one of the following curves represents the solution of the initial value problem dy/dx= 100-y, where y (0) = 50 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (More Than One Correct Option Type Questions)
13 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Statement I And Ii Type Questions)
9 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise For Session 5
8 Videos
- DETERMINANTS BOOK - ARIHANT MATHSCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
Similar Questions
The differential equation xdydx+3dydx=y2
View SolutionStatement I Differential equation corresponding to all lines, ax+by+c=0 has the order 3.
Statement II Gereral solution of a differential equation of nth order contains n independent arbitaray constanis.
View SolutionShow that the curve for which the normal at every point passes through a fixed point is a circle.
View SolutionIf a2+b2+c2=−2, and f(x)= ∣∣ ∣ ∣∣1+a2x(1+b2)x(1+c2)x(1+a2)x1+b2x(1+c2)x(1+a2)x(1+b2)x1+c2x∣∣ ∣ ∣∣ , then f(x) is a polynomial of degree
View SolutionThe functions f(x)−ex+x, being differentiable and one-one, has a differentiable inverse f−1(x) The value of ddxf−1 at the point f(log2) is
View SolutionSolve the initial vale problem dydx+2y2=0, y(1)=1 and find the corresponding solution curve.
View SolutionSolve the initial value problem: (x+1)dydx=2e−y−1, y(0)=0
View SolutionSolve the following initial value problems: (x−y)(dx+dy)=dx−dy, y(0)=−1
View SolutionFind the particular solution to the following initial value problem dydx=4xy,y(0)=1
View SolutionSolve the following initial value problems and find the corresponding solution curves :
y'+2y2=0,y(1)=1
View SolutionSolve the following initial value problems and find the corresponding solution curves :
y'=2xy,y(0)=1.
View SolutionSolve the following initial value problems and find the corresponding solution curves :
xdy+ydx=xydx,y(1)=1
View SolutionSolve the following initial value problems and find the corresponding solution curves :
x(xdy−ydx)=ydx,y(1)=1.
View SolutionSolve the following initial value problems :
dydx=2x+y, given that x=0,y=0.
View SolutionSolve the initial value problem dydx+2y2=0, y(1)=1 and find the corresponding solution curve.
View SolutionSolve the following initial value problem: xydydx=y+2, y(2)=0
View Solution
